题目内容
9.己知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的斜边上的高为( )| A. | 12 | B. | 6 | C. | 5 | D. | $\frac{12}{5}$ |
分析 先求出方程的两根,再由勾股定理求出斜边长,然后运用直角三角形的面积求出这个直角三角形斜边上的高即可.
解答 解:x2-7x+12=0,
方程左边因式分解得:(x-3)(x-4)=0,
解得:x=3或x=4,
∵方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,
∴斜边长=$\sqrt{{3}^{2}+{4}^{2}}$=5,
设这个直角三角形的斜边上的高为h,
根据题意得:$\frac{1}{2}$×5×h=$\frac{1}{2}$×3×4,
解得:h=$\frac{12}{5}$.
故选:D.
点评 本题考查了一元二次方程方程的解法、勾股定理、直角三角形面积的计算方法;熟练掌握一元二次方程方程的解法和勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
19.已知梯形ABCD中,AD∥BC,则∠A:∠B:∠C:∠D不可能是( )
| A. | 3:7:5:5 | B. | 5:4:5:4 | C. | 4:5:6:3 | D. | 8:1:4:5 |
20.下列各式正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-7)^{2}}$=7 | C. | $\root{3}{9}$=3 | D. | (-$\sqrt{2}$)2=4 |
14.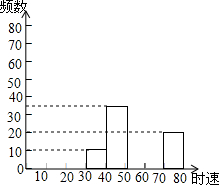 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
 小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:
小明将我市交通部门在某雷达测速区监测到的一组汽车的时速数据进行收集、整理,制作成如下不完整的统计图表,根据提供的信息解答下列问题:(1)把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速大于或等于60千米即为违章,则违章车辆共有多少辆?
| 时速x(km/h) | 频 数 | 频 率 |
| 30≤x≤40 | 10 | 0.05 |
| 40≤x≤50 | 36 | 0.18 |
| 50≤x≤60 | 78 | 0.39 |
| 60≤x≤70 | 56 | 0.28 |
| 70≤x≤80 | 20 | 0.10 |
| 总 计 | 200 | 1 |
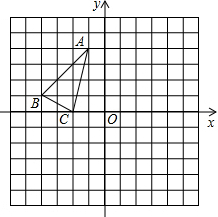 在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,4),B(-4,1),C(-2,0).
在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,4),B(-4,1),C(-2,0).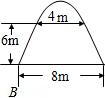 如图,某学校的校门是一抛物线形状的建筑物,地面宽度为8m,两侧距地面6m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为4m,则校门的高度为8m.
如图,某学校的校门是一抛物线形状的建筑物,地面宽度为8m,两侧距地面6m高处各有一个挂校名横匾用的铁环,两铁环的水平距离为4m,则校门的高度为8m.



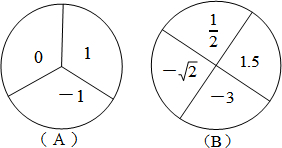
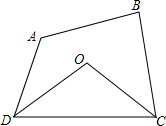 如图,在四边形ABCD中,∠A+∠B=210°,且∠ADC与∠DCB的平分线相交于O,求∠COD的度数.
如图,在四边形ABCD中,∠A+∠B=210°,且∠ADC与∠DCB的平分线相交于O,求∠COD的度数.