题目内容
在△ABC中，点M是AB边的中点，点E是BC上一点，AC的延长线与ME的延长线交于点F，若CE：EB=1：3，则AC：AF=考点：相似三角形的判定与性质
专题：
分析：过E作EH∥AB交AF于H，由已知条件可求出CH：AH的值，进而可求出HF：AH的值，再由已知条件点M是AB边的中点，即可求出AC：AF的值．
解答：
解：过E作EH∥AB交AF于H，
∵CE：EB=1：3，
∴EH：AB=1：4，CH：AC=1：4，
∴CH：AC=1：4，
∵点M是AB边的中点，
∴EH：AM=HF：AH=1：2，
∴AC：AF=2：3，
故答案为：2：3．
解：过E作EH∥AB交AF于H，∵CE：EB=1：3，
∴EH：AB=1：4，CH：AC=1：4，
∴CH：AC=1：4，
∵点M是AB边的中点，
∴EH：AM=HF：AH=1：2，
∴AC：AF=2：3，
故答案为：2：3．
点评：本题考查了相似三角形的判定和性质以及中点的定义，解题的关键是过E作EH∥AB交AF于H，构造相似三角形．
练习册系列答案
相关题目
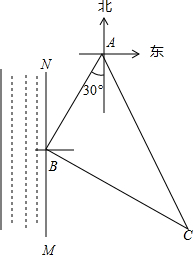如图，小明的家位于一条南北走向的河流MN的东侧A处，某一天小明从家出发沿南偏西30°方向走60m到达河边B处取水，然后沿另一方向走80m到达菜地C处浇水，最后沿第三方向走100m回到家A处．问小明在河边B处取水后是沿哪个方向行走的？并说明理由．
如图，半径为6cm的⊙O中，C、D为直径AB的三等分点，点E、F分别在AB两侧的半圆上，∠BCE=∠BDF=60°，连接AE、BF，则图中两个阴影部分的面积为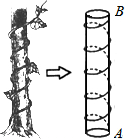
我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是
已知如图：△ABC、△DCE均为等腰直角三角形，其中AC=BC，DC=DE，∠ACB=∠D=90°，将△DCE绕点C旋转，两边分别交AB于M、N．若AM=3，BN=4，则△CMN的面积为
如图，按此规律，第6行最后一个数字是
如图，二次函数y=ax2+bx（a＜0）的图象过坐标原点O，与x轴的负半轴交于点A，过A点的直线与y轴交于B，与二次函数的图象交于另一点C，且C点的横坐标为-1，AC：BC=3：1．