题目内容
 如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为-1,AC:BC=3:1.
如图,二次函数y=ax2+bx(a<0)的图象过坐标原点O,与x轴的负半轴交于点A,过A点的直线与y轴交于B,与二次函数的图象交于另一点C,且C点的横坐标为-1,AC:BC=3:1.(1)求点A的坐标;
(2)设二次函数图象的顶点为F,其对称轴与直线AB及x轴分别交于点D和点E,若△FCD与△AED相似,求此二次函数的关系式.
考点:二次函数综合题
专题:几何综合题
分析:(1)过点C作CM∥OA交y轴于M,则△BCM∽△BAO,根据相似三角形对应边成比例得出
=
=
,即OA=4CM=4,由此得出点A的坐标为(-4,0);
(2)先将A(-4,0)代入y=ax2+bx,化简得出b=4a,即y=ax2+4ax,则顶点F(-2,-4a),设直线AB的解析式为y=kx+n,将A(-4,0)代入,化简得n=4k,即直线AB的解析式为y=kx+4k,则B点(0,4k),D(-2,2k),C(-1,3k).由C(-1,3k)在抛物线y=ax2+4ax上,得出3k=a-4a,化简得到k=-a.再由△FCD与直角△AED相似,则△FCD是直角三角形,又∠FDC=∠ADE<90°,∠CFD<90°,得出∠FCD=90°,△FCD∽△AED.再根据两点之间的距离公式得出FC2=CD2=1+a2,得出△FCD是等腰直角三角形,则△AED也是等腰直角三角形,所以∠DAE=45°,由三角形内角和定理求出∠OBA=45°,那么OB=OA=4,即4k=4,求出k=1,a=-1,进而得到此二次函数的关系式为y=-x2-4x.
| CM |
| OA |
| BC |
| AB |
| 1 |
| 4 |
(2)先将A(-4,0)代入y=ax2+bx,化简得出b=4a,即y=ax2+4ax,则顶点F(-2,-4a),设直线AB的解析式为y=kx+n,将A(-4,0)代入,化简得n=4k,即直线AB的解析式为y=kx+4k,则B点(0,4k),D(-2,2k),C(-1,3k).由C(-1,3k)在抛物线y=ax2+4ax上,得出3k=a-4a,化简得到k=-a.再由△FCD与直角△AED相似,则△FCD是直角三角形,又∠FDC=∠ADE<90°,∠CFD<90°,得出∠FCD=90°,△FCD∽△AED.再根据两点之间的距离公式得出FC2=CD2=1+a2,得出△FCD是等腰直角三角形,则△AED也是等腰直角三角形,所以∠DAE=45°,由三角形内角和定理求出∠OBA=45°,那么OB=OA=4,即4k=4,求出k=1,a=-1,进而得到此二次函数的关系式为y=-x2-4x.
解答:解:(1)如图,过点C作CM∥OA交y轴于M.
∵AC:BC=3:1,
∴
=
.
∵CM∥OA,
∴△BCM∽△BAO,
∴
=
=
=
,
∴OA=4CM=4,
∴点A的坐标为(-4,0);

(2)∵二次函数y=ax2+bx(a<0)的图象过A点(-4,0),
∴16a-4b=0,
∴b=4a,
∴y=ax2+4ax,对称轴为直线x=-2,
∴F点坐标为(-2,-4a).
设直线AB的解析式为y=kx+n,将A(-4,0)代入,
得-4k+n=0,
∴n=4k,
∴直线AB的解析式为y=kx+4k,
∴B点坐标为(0,4k),D点坐标为(-2,2k),C点坐标为(-1,3k).
∵C(-1,3k)在抛物线y=ax2+4ax上,
∴3k=a-4a,
∴k=-a.
∵△AED中,∠AED=90°,
∴若△FCD与△AED相似,则△FCD是直角三角形,
∵∠FDC=∠ADE<90°,∠CFD<90°,
∴∠FCD=90°,
∴△FCD∽△AED.
∵F(-2,-4a),C(-1,3k),D(-2,2k),k=-a,
∴FC2=(-1+2)2+(3k+4a)2=1+a2,CD2=(-2+1)2+(2k-3k)2=1+a2,
∴FC=CD,
∴△FCD是等腰直角三角形,
∴△AED是等腰直角三角形,
∴∠DAE=45°,
∴∠OBA=45°,
∴OB=OA=4,
∴4k=4,
∴k=1,
∴a=-1,
∴此二次函数的关系式为y=-x2-4x.
∵AC:BC=3:1,
∴
| BC |
| AB |
| 1 |
| 4 |
∵CM∥OA,
∴△BCM∽△BAO,
∴
| CM |
| OA |
| BC |
| AB |
| 1 |
| 4 |
| BM |
| OB |
∴OA=4CM=4,
∴点A的坐标为(-4,0);

(2)∵二次函数y=ax2+bx(a<0)的图象过A点(-4,0),
∴16a-4b=0,
∴b=4a,
∴y=ax2+4ax,对称轴为直线x=-2,
∴F点坐标为(-2,-4a).
设直线AB的解析式为y=kx+n,将A(-4,0)代入,
得-4k+n=0,
∴n=4k,
∴直线AB的解析式为y=kx+4k,
∴B点坐标为(0,4k),D点坐标为(-2,2k),C点坐标为(-1,3k).
∵C(-1,3k)在抛物线y=ax2+4ax上,
∴3k=a-4a,
∴k=-a.
∵△AED中,∠AED=90°,
∴若△FCD与△AED相似,则△FCD是直角三角形,
∵∠FDC=∠ADE<90°,∠CFD<90°,
∴∠FCD=90°,
∴△FCD∽△AED.
∵F(-2,-4a),C(-1,3k),D(-2,2k),k=-a,
∴FC2=(-1+2)2+(3k+4a)2=1+a2,CD2=(-2+1)2+(2k-3k)2=1+a2,
∴FC=CD,
∴△FCD是等腰直角三角形,
∴△AED是等腰直角三角形,
∴∠DAE=45°,
∴∠OBA=45°,
∴OB=OA=4,
∴4k=4,
∴k=1,
∴a=-1,
∴此二次函数的关系式为y=-x2-4x.
点评:本题是二次函数的综合题型,其中涉及到相似三角形、等腰直角三角形的判定与性质,运用待定系数法求二次函数、一次函数的解析式,两点之间的距离公式、抛物线对称轴的求法,函数图象上点的坐标特征.综合性较强,有一定难度.(2)中得出△FCD是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
若α,β是方程x2-2x-3=0的两个实数根,则α2+β2的值为( )
| A、10 | B、9 | C、7 | D、5 |
 在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF=
在△ABC中,点M是AB边的中点,点E是BC上一点,AC的延长线与ME的延长线交于点F,若CE:EB=1:3,则AC:AF= 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.求证:MD=ME.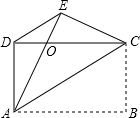 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
 如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是
如图,点A、B、C都在圆O上,如果∠AOB+∠ACB=84°,那么∠ACB的大小是