题目内容
直线a:y=x+2和直线b:y=-x+4相交于点A,分别与x轴相交于点B和点C,与y轴相交于点D和点E.
(1)求△ABC的面积;
(2)求四边形ADOC的面积.
(1)求△ABC的面积;
(2)求四边形ADOC的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)首先求得两直线与坐标轴的交点坐标和两直线的交点坐标,然后即可求△ABC的面积;
(2)作AE⊥x轴于点E,利用S四边形ADOC=S梯形DOEA+S△AEC求解.
(2)作AE⊥x轴于点E,利用S四边形ADOC=S梯形DOEA+S△AEC求解.
解答: 解:(1)令y=x+2=0,解得:x=-2,
解:(1)令y=x+2=0,解得:x=-2,
令x=0,解得:x=2,
∴B(-2,0),D(0,2);
令y=-x+4=0,解得:x=4,
令x=0,解得:y=4,
∴C(4,0),E(0,4),
由
解得:
∴A(1,3)
∴BC=4-(-2)=6,
∴△ABC的面积为
×6×3=9;
(2)作AE⊥x轴于点E,
S四边形ADOC=S梯形DOEA+S△AEC=
(DO+AE)•OE+
AE•EC=
(2+3)×1+
×3×3=7.
 解:(1)令y=x+2=0,解得:x=-2,
解:(1)令y=x+2=0,解得:x=-2,令x=0,解得:x=2,
∴B(-2,0),D(0,2);
令y=-x+4=0,解得:x=4,
令x=0,解得:y=4,
∴C(4,0),E(0,4),
由
|
解得:
|
∴A(1,3)
∴BC=4-(-2)=6,
∴△ABC的面积为
| 1 |
| 2 |
(2)作AE⊥x轴于点E,
S四边形ADOC=S梯形DOEA+S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了两直线平行或相交的问题,解题的关键是求得直线与坐标轴的交点坐标和两直线的交点坐标.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知a的倒数是-
,则a是( )
| 1 |
| 3 |
A、
| ||
| B、-3 | ||
C、-
| ||
| D、3 |
如果关于x的不等式(a+2)x>a+2的解集为x<1,那么a的取值范围是( )
| A、a>0 | B、a<0 |
| C、a>-2 | D、a<-2 |
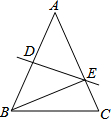 如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )
如图,将△ABC沿直线DE折叠,使得点A与点B重合,已知AC=8cm,△BCE的周长为13cm,则BC的长为( )| A、5cm | B、6cm |
| C、8cm | D、10cm |