题目内容
2. 如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.
如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.(1)求BC的长;
(2)利用此图形求tan15°的值(精确到0.1,参考数据:$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{5}$=2.2)
分析 (1)过A作AD⊥BC,交BC的延长线于点D,由含30°的直角三角形性质得AD=$\frac{1}{2}$AC=2,由三角函数求出CD=2$\sqrt{3}$,在Rt△ABD中,由三角函数求出BD=16,即可得出结果;
(2)在BC边上取一点M,使得CM=AC,连接AM,求出∠AMC=∠MAC=15°,tan15°=tan∠AMD=$\frac{AD}{MD}$即可得出结果.
解答 解: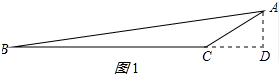 (1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
在Rt△ADC中,AC=4,
∵∠C=150°,
∴∠ACD=30°,
∴AD=$\frac{1}{2}$AC=2,
CD=AC•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
在Rt△ABD中,tanB=$\frac{AD}{BD}$=$\frac{2}{BD}$=$\frac{1}{8}$,
∴BD=16,
∴BC=BD-CD=16-2$\sqrt{3}$;
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD=$\frac{AD}{MD}$=$\frac{2}{4+2\sqrt{3}}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$≈0.27≈0.3.
点评 本题考查了锐角三角函数、含30°的直角三角形性质、三角形的内角和、等腰三角形的性质等知识;熟练掌握三角函数运算是解决问题的关键.

练习册系列答案
相关题目
13.有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
| A. | $\frac{1}{2}$x(x-1)=45 | B. | $\frac{1}{2}$x(x+1)=45 | C. | x(x-1)=45 | D. | x(x+1)=45 |
14.实数a、b满足$\sqrt{a+1}$+4a2+4ab+b2=0,则ba的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
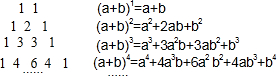 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):