Question

12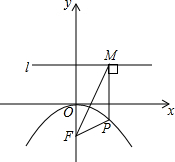．如图，抛物线的顶点是原点，抛物线经过A点（8，-8），F点坐标为（0，-2），直线l为y=2，直线l平行于x轴．P点是抛物线上任意一点，过P点作PM⊥l，垂足为M点．
（1）求抛物线的函数关系式；
（2）求证：∠PFM=∠PMF；
（3）当三角形MPF是等腰直角三角形时，求P点的坐标．

Answer 1

分析 （1）利用待定系数法即可直接求得二次函数的解析式；
（2）设P的坐标是（x，-$\frac{1}{8}$x²），利用x表示出PM和PF的长，证明PM=PF，根据等边对等角即可证得；
（3）当△MPF是等腰直角三角形时，根据PM=PF即可列方程求得P的横坐标．

解答 （1）解：∵二次函数的顶点是原点，
∴设二次函数的解析式是y=ax²，
∴将点A（8，-8）代入得a=-$\frac{1}{8}$，
则二次函数的解析式是y=-$\frac{1}{8}$x²；
（2）证明：∵点P在抛物线y=-$\frac{1}{8}$x²上，
∴设P的坐标是（x，-$\frac{1}{8}$x²），
过点P作PB⊥y轴于点B．
则BF=-2-（-$\frac{1}{8}$x²）=$\frac{1}{8}$x²-2，PB=x．
∴直角△BPF中，PF=$\sqrt{（\frac{1}{8}{x}^{2}-2）^{2}+{x}^{2}}$=$\frac{1}{8}$x²+2．
∵PM⊥直线y=2，
∴PM=$\frac{1}{8}$x²+2，
∴PF=PM，
∴∠PFM=∠PMF；
（3）解：当△MPF是等腰直角三角形时，
PF⊥PM，PF=PM．
设P的横坐标是x，则2-（-$\frac{1}{8}$x²）=x，
解得：x=4，
则P的坐标是（4，-2）．
同理，当P第三象限时，坐标是（-4，-2）．
总之，P的坐标是（4，-2）或（-4，-2）．

点评 本题考查了待定系数法求二次函数解析式，以及等腰三角形的性质，正确利用P的横坐标表示出PM和PF的长是关键．