Question

2．（1）等边△ABC外一点D，且∠BDC=120°，试探索∠BDA与∠CDA的数量关系；
（2）将等边△ABC改为等腰直角△ABC，∠BAC=90°，结合（1）所给图形试修改（1）中的条件，使得（1）的结论依然成立，补充图形并证明．
（3）将等边△ABC改为一般的等腰△ABC，且∠BAC=α，则如何修改（1）中的条件，使得（1）的结纶依然成立，补充图形并证明．

Answer 1

分析 （1）过A作AM⊥DB于M，AN⊥CD于N，证△AMB≌△ANC，推出AM=AN，根据角平分线性质得出即可；
（2）当∠BDC=90°时，（1）的结论依然成立，如图2，过A作AM⊥DB于M，AN⊥CD于N，则∠M=∠ANC=90°，推出△AMB≌△ANC（AAS），根据全等三角形的性质得到AM=AN，根据角平分线的性质即可得到结论；
（3）当∠BDC=180°-α时，（1）的结论依然成立，如图3，过A作AM⊥DB于M，AN⊥CD于N，则∠M=∠ANC=90°，推出△AMB≌△ANC（AAS），根据全等三角形的性质得到AM=AN，根据角平分线的性质即可得到结论．

解答 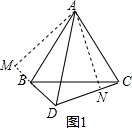解：（1）∠BDA=∠CDA，
理由是：如图1，过A作AM⊥DB于M，AN⊥CD于N，
则∠M=∠ANC=90°，
∵∠BAC=60°，∠BDC=120°，
∴∠ABD+∠ACD=360°-120°-60°=180°，
∵∠ABD+∠ABM=180°，
∴∠ACN=∠ABM，
在△AMB和△ANC中，
$\left\{\begin{array}{l}{∠ABM=∠ACN}\\{∠M=∠ANC}\\{AB=AC}\end{array}\right.$，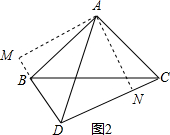
∴△AMB≌△ANC（AAS），
∴AM=AN，
∵AM⊥DB，AN⊥CD，
∴∠BDA=∠CDA；

（2）当∠BDC=90°时，（1）的结论依然成立，
如图2，过A作AM⊥DB于M，AN⊥CD于N，
则∠M=∠ANC=90°，
∵∠BAC=90°，∠BDC=90°，
∴∠ABD+∠ACD=360°-90°-90°=180°，
∵∠ABD+∠ABM=180°，
∴∠ACN=∠ABM，
在△AMB和△ANC中，
$\left\{\begin{array}{l}{∠ABM=∠ACN}\\{∠M=∠ANC}\\{AB=AC}\end{array}\right.$，
∴△AMB≌△ANC（AAS），
∴AM=AN，
∵AM⊥DB，AN⊥CD，
∴∠BDA=∠CDA；

（3）当∠BDC=180°-α时，（1）的结论依然成立，
如图3，过A作AM⊥DB于M，AN⊥CD于N，
则∠M=∠ANC=90°，
∵∠BAC=α°，∠BDC=180°-α，
∴∠ABD+∠ACD=180°，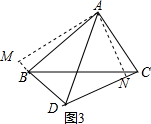
∵∠ABD+∠ABM=180°，
∴∠ACN=∠ABM，
在△AMB和△ANC中，
$\left\{\begin{array}{l}{∠ABM=∠ACN}\\{∠M=∠ANC}\\{AB=AC}\end{array}\right.$，
∴△AMB≌△ANC（AAS），
∴AM=AN，
∵AM⊥DB，AN⊥CD，
∴∠BDA=∠CDA．

点评 本题考查了全等三角形的性质和判定，角平分线性质，正确的作出辅助线构造全等三角形是解题的关键．