题目内容
11.已知a,b,c都是质数,并且a+b+c+ab+bc+ac=133,则abc=154.分析 质数中除2外都是奇数,奇数+奇数=偶数,a+b+c+ab+bc+ac=133,其中a、b、c都是质数,ab、bc、ac都是奇数,如果这6个奇数中没有偶数,结果不可能是奇数(133),因此这三个质数中必有偶数2.假设a=2,则2+b+c+2b+2c+bc=133,即3(b+c)+bc=131,(b+3)(c+3)=140=22×5×7,b+3=10,c+3=14,b=7,c=11,然后即可求出abc.
解答 解:因为a、b、c都是质数
如果a、b、c中没有2,那么a+b+c+ab+bc+ac≠133
所以必有2
设a=2
2+b+c+2b+2c+bc=133
3(b+c)+bc=131
(b+3)(c+3)=140=22×5×7
b+3=10
c+3=14
b=7
c=11
abc=2×7×11=154.
故答案为:154.
点评 此题考查了质数与合数的知识,解答此题的难点是确定a、b、c都是质数分别是多少.根据质数的特征,及奇数+奇数=偶数,偶数+偶数=偶数,即可求得三个质数分别是多少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列关于矩形的说法,正确的是( )
| A. | 对角线相等的四边形是矩形 | B. | 对角线互相平分的四边形是矩形 | ||
| C. | 矩形的对角线相等且互相平分 | D. | 矩形的对角线互相垂直且平分 |
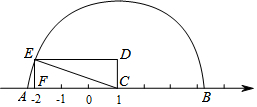 如图所示,数轴上点C表示的数是1,点F表示的数是-2,CD=1,以CD,CF为边作长方形CDEF,以C为圆心、CE的长为半径画弧交数轴于A、B两点,则点A表示的数是1-$\sqrt{10}$,点B表示的数是1+$\sqrt{10}$.
如图所示,数轴上点C表示的数是1,点F表示的数是-2,CD=1,以CD,CF为边作长方形CDEF,以C为圆心、CE的长为半径画弧交数轴于A、B两点,则点A表示的数是1-$\sqrt{10}$,点B表示的数是1+$\sqrt{10}$. 如图,要使输出值y大于100,则输入的最小正整数x是20.
如图,要使输出值y大于100,则输入的最小正整数x是20. 如图,已知∠B=∠C,点B,A,D在同一直线上,AE平分∠DAC,说明AE∥BC的理由.
如图,已知∠B=∠C,点B,A,D在同一直线上,AE平分∠DAC,说明AE∥BC的理由. 如图,A点的位置是东偏北40°,距离O点3km.
如图,A点的位置是东偏北40°,距离O点3km.