题目内容
20.(1)$\sqrt{\frac{1}{8}}$+$\sqrt{18}$-$\sqrt{8}$(2)(2$\sqrt{\frac{1}{6}}$-$\sqrt{24}$)÷$\sqrt{2}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先利用二次根式的除法法则运算,然后化简后合并即可.
解答 解:(1)原式=$\frac{\sqrt{2}}{4}$+3$\sqrt{2}$-2$\sqrt{2}$
=$\frac{5\sqrt{2}}{4}$;
(2)原式=2$\sqrt{\frac{1}{6}×\frac{1}{2}}$-$\sqrt{24×\frac{1}{2}}$
=$\frac{\sqrt{3}}{3}$-2$\sqrt{3}$
=-$\frac{5\sqrt{3}}{3}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
10. 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
 如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )
如图,△ABC为⊙O的内接三角形,∠BOC=80°,则∠A等于( )| A. | 80 | B. | 60 | C. | 50 | D. | 40 |
15.用四舍五入法按要求对0.05019分别去近似值,其中错误的是( )
| A. | 0.1(精确到0.1) | B. | 0.05(精确到百分位) | ||
| C. | 0.0501(精确到0.0001) | D. | 0.0502(精确到0.0001) |
5.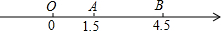 如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
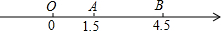 如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )
如图,点O、A、B在数轴上,分别表示数0、1.5、4.5,数轴上另有一点C,到点A的距离为1,到点B的距离小于3,则点C位于( )| A. | 点O的左边 | B. | 点O与点A之间 | C. | 点B的右边 | D. | 点A与点B之间 |
12.一条铁路上有10个站,则共需要制( )种火车票.
| A. | 45 | B. | 55 | C. | 90 | D. | 110 |