Question

15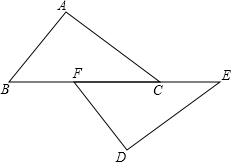．已知如图，点B、F、C、E、在一条直线上，AB⊥AC，DE⊥DF，AC=DF，BF=CE．求证：AB∥DE．

Answer 1

分析 求出BC=EF，∠A=∠D=90°，根据HL推出Rt△BAC≌Rt△EDF，根据全等三角形的性质得出∠B=∠E，根据平行线的判定得出即可．

解答 证明：∵BF=CE，
∴BF+FC=CE+FC，
∴BC=EF，
∵AB⊥AC，DE⊥DF，
∴∠A=∠D=90°，
在Rt△BAC和Rt△EDF中
$\left\{\begin{array}{l}{BC=EF}\\{AC=DF}\end{array}\right.$
∴Rt△BAC≌Rt△EDF（HL），
∴∠B=∠E，
∴AB∥DE．

点评 本题考查了全等三角形的性质和判定，平行线的判定的应用，能推出△BAC和△EDF全等是解此题的关键．