题目内容
19.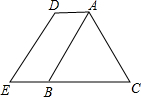 如图,在△ABC中,AB=AC,AC+BC=14,将△ABC边沿CB方向向左平移$\frac{1}{2}$BC的长,连接AD、BE、DE,求四边形ACED的周长.
如图,在△ABC中,AB=AC,AC+BC=14,将△ABC边沿CB方向向左平移$\frac{1}{2}$BC的长,连接AD、BE、DE,求四边形ACED的周长.
分析 根据平移的性质,即可证得AD∥EC,ED=AC,即可证得四边形ACED是等腰梯形;根据BE=AD=$\frac{1}{2}$BC,则AD+BE=BC即可求解.
解答 解:根据平移的性质,可得AD∥EC,ED=AC
又∵AD≠EC,AB=AC
∴四边形ACED是等腰梯形.
∵BE=AD=$\frac{1}{2}$BC
∴AD+BE=BC
又∵DE=AC
∴AD+DE+BE=AC+BC=14.
∴四边形ACED的周长是:AD+DE+BE+AC+BC=2(AC+BC)=28.
点评 本题主要考查了等腰梯形的定义,正确理解平移的性质,求得BE=AD=$\frac{1}{2}$BC,即AD+BE=BC是解决本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
8.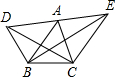 如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
 如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )
如图,已知A是DE的中点,设△DBC,△ABC,△EBC的面积分别为S1,S2,S3,则S1,S2,S3的关系为( )| A. | ${S_2}=\frac{3}{2}({S_1}+{S_3})$ | B. | ${S_2}=\frac{1}{2}({S_3}-{S_1})$ | C. | ${S_2}=\frac{1}{2}({S_1}+{S_3})$ | D. | ${S_2}=\frac{3}{2}({S_3}-{S_1})$ |
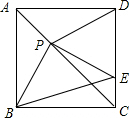 如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.
如图,正方形ABCD中,对角线AC上有一点P,连接BP、DP,过点P作PE⊥PB交CD于点E,连接BE.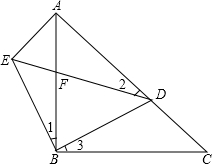 如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,
如图,三角形ABC,AB=BC,∠ABC=90°,∠1=∠2=∠3,