��Ŀ����
19�����Ķ����в��ϣ����⣺��֪����x2+x-1=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
�⣺�����̵ĸ�Ϊy����y=2x������x=$\frac{y}{2}$��
��x=$\frac{y}{2}$������֪���̣��ã�$\frac{y}{2}$��2+$\frac{y}{2}$-1=0��
����y2+2y-4=0
������Ϊy2+2y-4=0��
�������÷��̵Ĵ������·��̵ķ��������dz�Ϊ������������
�����Ķ������ṩ�ġ������������·��̣�Ҫ�����̻�Ϊһ����ʽ����
��1����֪����x2+x-2=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����������Ϊ��y2-y-2=0��
��2����֪����2x2-7x+3=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸��ĵ�����
��3����֪����x��һԪ���η���ax2+bx+c=0��a��0��������ʵ�����ֱ�Ϊ3��-2����һԪ���η���cx2+bx+a=0����������ֱ��д�������
���� ��1���������⣬�����̵ĸ���y����y=-x������x=-y��Ȼ���x=-y����ԭ���̣��������
��2���������⣬�����̵ĸ���y����y=$\frac{1}{x}$������x=$\frac{1}{y}$��Ȼ���x=$\frac{1}{y}$����ԭ���̣��������
��3���ɣ�2����֪���Է���cx2+bx+a=0����ͬʱ����x2����a��$\frac{1}{x}$��2-7•$\frac{1}{x}$+c=0����cx2+bx+a=0��������ax2+bx+c=0��a��0�������ĵ�����������⣮
��� �⣺��1�������̵ĸ���y����y=-x������x=-y��
��x=-y����x2+x-2=0����y2-y-2=0��
�ʴ���y2-y-2=0��
�ʴ�Ϊy2-y-2=0��
��2�������̵ĸ���y����y=$\frac{1}{x}$������x=$\frac{1}{y}$��
��x=$\frac{1}{y}$���뷽��2x2-7x+3=0����2��$\frac{1}{y}$��2-7•$\frac{1}{y}$+3=0��
����3y2-7y+2=0��
��3���ɣ�2����֪���Է���cx2+bx+a=0����ͬʱ����x2��
��a��$\frac{1}{x}$��2-7•$\frac{1}{x}$+c=0��
��cx2+bx+a=0��������ax2+bx+c=0��a��0�������ĵ�����
���Է���cx2+bx+a=0�������ֱ���$\frac{1}{3}$��-$\frac{1}{2}$��
���� ���⿼����һԪ���η��̵Ľ⣬����ϵ���Ĺ�ϵ������Ĺؼ������ջ�������ʹ�ã�

| A�� | $\frac{1}{25}$��ƽ������$��\frac{1}{5}$ | B�� | -9��81��һ��ƽ���� | ||
| C�� | 0.2������ƽ������0.04 | D�� | 2������ƽ������$\sqrt{2}$ |
��1��������ӹ�x�죬�ּӹ�y�죬�����������
| ���ӹ� | �ּӹ� | |
| �ӹ����������죩 | x | y |
| ��õ�����Ԫ�� | 6000x | 8000y |
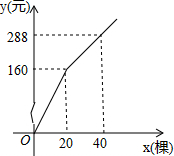 Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��
Ϊ���¹���Ʒ�֣�ij���ƻ��¹���A��B����Ʒ�ֵĹ�������ֲ���������ƻ����������ֹ����繲45�ã�����A����ĵ���Ϊ7Ԫ/�ã�����B�����������y��Ԫ���빺������x���ã�֮�������ͼ��ʾ�ĺ�����ϵ��