题目内容
13.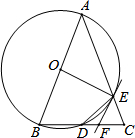 如图,AB是⊙O直径,AB=AC,BC、AC分别与⊙O相交于点D、E,EF是⊙O的切线,且与BC相交于点F.已知∠EDC=50°,则∠EFC=75°.
如图,AB是⊙O直径,AB=AC,BC、AC分别与⊙O相交于点D、E,EF是⊙O的切线,且与BC相交于点F.已知∠EDC=50°,则∠EFC=75°.
分析 由圆内接四边形的性质可知∠A=∠EDC=50°,由等腰三角形的性质可知∠OAE=∠AEO=50°,由切线的性质可知∠OEF=90°,从而可求得∠FEC=40°,由等腰三角形的性质可知∠C=65°,最后由三角形的内角和定理可知∠EFC=75°.
解答 解:∵四边形ABDE是圆内接四边形,
∴∠A=∠EDC=50°.
∵OA=OE,
∴∠OAE=∠AEO=50°.
∵EF是圆O的切线,
∴∠OEF=90°.
∴∠FEC=180°-∠AEO-∠OEF=180°-50°-90°=40°.
∵AB=AC,∠A=50°,
∴∠C=$\frac{1}{2}×(180-∠A)$=65°.
∴∠EFC=180°-∠C-∠FEC=180°-65°-40°=75°.
故答案为:75°.
点评 本题主要考查的是切线的性质、圆内接四边形的性质、等腰三角形的性质,求得∠FEC=40°、∠C=65°是解题的关键.

练习册系列答案
相关题目
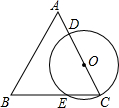 如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π).
如图,△ABC是等边三角形,点O在边AC上(不与A,C重合),以点O为圆心,以OC为半径的圆分别与AC、BC相交于点D、E,若OC=1,则$\widehat{DE}$的长是$\frac{2π}{3}$(结果保留π). 已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,BC=$\sqrt{6}$,BD=1.求AD=5.
已知:如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足是D,BC=$\sqrt{6}$,BD=1.求AD=5.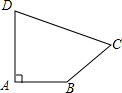 如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?
如图所示的四边形ABCD中,其中AB=3,BC=12,CD=13,DA=4,∠A=90°,你能求出四边形ABCD的面积吗?