题目内容
9.计算:(1)$\sqrt{18}-\sqrt{\frac{9}{2}}+{(1-\sqrt{2})^2}$
(2)${a^2}\sqrt{8a}+3a\sqrt{18{a^3}}$.
分析 (1)根据二次根式的加减法和完全平方公式可以解答本题;
(2)根据二次根式的加法可以解答本题.
解答 解:(1)$\sqrt{18}-\sqrt{\frac{9}{2}}+{(1-\sqrt{2})^2}$
=$3\sqrt{2}-\frac{3\sqrt{2}}{2}+1-2\sqrt{2}+2$
=$-\frac{\sqrt{2}}{2}+3$;
(2)${a^2}\sqrt{8a}+3a\sqrt{18{a^3}}$
=$2{a}^{2}\sqrt{2a}+9{a}^{2}\sqrt{2a}$
=11${a}^{2}\sqrt{2a}$.
点评 本题考查二次根式的加减法,解答本题的关键是明确二次根式加减法的计算方法.

练习册系列答案
相关题目
4.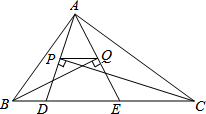 如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
 如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
如图,△ABC的周长为30,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )| A. | $\frac{3}{2}$ | B. | 5 | C. | 3 | D. | 4 |

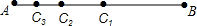 如图,线段AB=8cm,点C1为AB的中点,点C2为AC1的中点,点C3为AC2的中点…按照此规律,线段ACn的长为23-n.
如图,线段AB=8cm,点C1为AB的中点,点C2为AC1的中点,点C3为AC2的中点…按照此规律,线段ACn的长为23-n.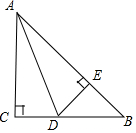 如图,在△ABC,∠C=90°,AD是∠ABC的角平分线,DE⊥AB,垂足为E,DE=EB.
如图,在△ABC,∠C=90°,AD是∠ABC的角平分线,DE⊥AB,垂足为E,DE=EB.