题目内容
19.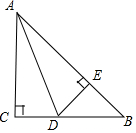 如图,在△ABC,∠C=90°,AD是∠ABC的角平分线,DE⊥AB,垂足为E,DE=EB.
如图,在△ABC,∠C=90°,AD是∠ABC的角平分线,DE⊥AB,垂足为E,DE=EB.求证:AC+CD=AB.
分析 只要证明△ACD≌△AED,即可推出AC=AE,CD=DE=BE,由此即可解决问题.
解答 证明:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴DE=CD.
在Rt△ACD与Rt△AED中,
∵$\left\{\begin{array}{l}{AD=AD}\\{DE=DC}\end{array}\right.$,
∴△ACD≌△AED,
∴AC=AE,CD=DE=BE,
∴AB=AE+EB=AC+CD.
点评 此题考查等腰直角三角形的性质,全等三角形的判定与性质,角平分线的性质等知识点的理解和掌握,证明此题的关键是证明△ACD≌△AED,此题难度不大,属于基础题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
14.下列代数式中,是分式的是( )
| A. | $\frac{x^2}{3}$ | B. | $\frac{5x}{π}$ | C. | $\frac{2}{x}$ | D. | $\frac{2}{3}$xy2+4 |
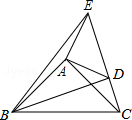 如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2<2(AD2+AB2).其中结论正确的个数是( )
如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2<2(AD2+AB2).其中结论正确的个数是( )