Question

18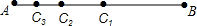．如图，线段AB=8cm，点C₁为AB的中点，点C₂为AC₁的中点，点C₃为AC₂的中点…按照此规律，线段AC_n的长为2^3-n．

Answer 1

分析 根据中点得定义分别得出AC₁=$\frac{1}{2}$AB=$\frac{1}{2}$×8、AC₂=$\frac{1}{2}$AC₁=（$\frac{1}{2}$）²×8、AC₃=$\frac{1}{2}$AC₂=（$\frac{1}{2}$）³×8，即可得出AC_n=（$\frac{1}{2}$）ⁿ×8=2^3-n．

解答 解：根据题意，得：AC₁=$\frac{1}{2}$AB=$\frac{1}{2}$×8，
AC₂=$\frac{1}{2}$AC₁=$\frac{1}{2}$×$\frac{1}{2}$AB=（$\frac{1}{2}$）²×8，
AC₃=$\frac{1}{2}$AC₂=$\frac{1}{2}$×$\frac{1}{2}$×$\frac{1}{2}$AB=（$\frac{1}{2}$）³×8，
…
AC_n=（$\frac{1}{2}$）ⁿ×8=2^-n•2³=2^3-n，
故答案为：2^3-n．

点评 本题主要考查两点间的距离，熟练掌握线段中点的定义及数字的变化规律是解题的关键．