题目内容
12.已知关于x的方程(m+3)x|m|-2+6m=0…①与nx-5=x(3-n)…②的解相同,其中方程①是一元一次方程,求代数式(m+x+1)2016•(-m2n+xn2)+1的值.分析 根据一元一次方程的定义,未知项的次数为1,系数不为0,可先求得m和x的值,再根据方程的解的定义,求出n的值,最后代入求代数式的值.
解答 解:因为①是一元一次方程,所以|m|-2=1且m+3≠0,解得m=3.
∴方程①变为6x+18=0,
解得x=-3,
又①与②的解相同,代入得-3n-5=-3(3-n),
解得:n=$\frac{2}{3}$.
当m=3,x=-3,n=$\frac{2}{3}$时,
(m+x+1)2016•(-m2n+xn2)+1,
=(3-3+1)2016•(-32×$\frac{2}{3}$-3×$\frac{4}{9}$)+1,
=-6-$\frac{4}{3}$+1,
=-$\frac{19}{15}$.
点评 本题既考查了同解方程的定义:如果第一个方程的解都是第二个方程的解,并且第二个方程的解也都是第一个方程的解,那么这两个方程叫做同解方程.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3.下列各组数中,互为相反数的是( )
| A. | -34与(-3)4 | B. | -23与(-2)3 | C. | 102与210 | D. | -(-4)与|-4| |
 如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm
如图,已知线段AB,点E、F分别是线段AC、BD的中点,CD=4cm,AC+BD=10cm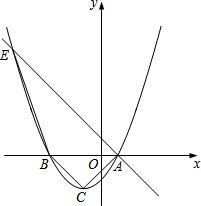 如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.
如图,设抛物线y=ax2+x+c与x轴交于两个不同的点A(1,0)、B(m,0),对称轴为直线x=-1,顶点记为点C.且∠ACB=90°.