题目内容
20.关于x的一元二次方程x2-2(m+1)x+m2+5=0有两个实数根.(1)求m的取值范围.
(2)如果等腰三角形ABC的两边是这个方程的两根,且腰长是7,求这个三角形的周长.
分析 (1)利用判别式的意义得到△=4(m+1)2-4(m2+5)≥0,然后解不等式即可;
(2)利用等腰三角形的性质得到方程的一个解为7,把x=7代入x2-2(m+1)x+m2+5=0得m1=10,m2=4,讨论:当m=10时,方程化为x2-22x+105=0;当m=4时,方程化为x2-10x+21=0,然后分别解方程后利用三角形三边的关系确定三角形三边,最后就是三角形的周长.
解答 解:(1)根据题意得△=4(m+1)2-4(m2+5)≥0,
解得m≥2;
(2)把x=7代入x2-2(m+1)x+m2+5=0得49-2(m+1)+m2+5=0,解得m1=10,m2=4,
当m=10时,方程化为x2-22x+105=0,解得x1=7,x2=15,而7+7<15,故舍去;
当m=4时,方程化为x2-10x+21=0,解得x1=7,x2=3,此时三角形周长为3+7+7=17.
所以三角形的周长为17.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.也考查了三角形三边的关系.

练习册系列答案
相关题目
15. 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 12 |
12.为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如表所示:
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
| 甲 | 63 | 66 | 63 | 61 | 64 | 61 |
| 乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(2)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
9.对于二次函数y=-(x-1)2+2的图象与性质,下列说法正确的是( )
| A. | 对称轴是直线x=1,最小值是2 | B. | 对称轴是直线x=1,最大值是2 | ||
| C. | 对称轴是直线x=-1,最小值是2 | D. | 对称轴是直线x=-1,最大值是2 |
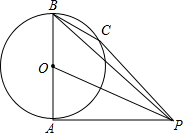 如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.
如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.