题目内容
关于x的一元二次方程（k-1）x2-2x+3=0有实数根．
（1）求k的取值范围；
（2）求整数k的最大值，并计算k取最大值时方程的根．
（1）求k的取值范围；
（2）求整数k的最大值，并计算k取最大值时方程的根．
考点：根的判别式,一元二次方程的定义
专题：
分析：（1）根据已知得出k-1≠0，b2-4ac=（-2）2-4（k-1）×3≥0，求出不等式组的解集即可；
（2）求出k的值，代入，求出方程的解即可．
（2）求出k的值，代入，求出方程的解即可．
解答：解：（1）∵关于x的一元二次方程（k-1）x2-2x+3=0有实数根，
∴k-1≠0，b2-4ac=（-2）2-4（k-1）×3≥0，
解得：k＜1，
即k的取值范围是k＜1；
（2）∵k＜1，
∴最大整数值是k=0，
代入方程得：-x2-2x+3=0，
解得：x1=-3，x2=1．
∴k-1≠0，b2-4ac=（-2）2-4（k-1）×3≥0，
解得：k＜1，
即k的取值范围是k＜1；
（2）∵k＜1，
∴最大整数值是k=0，
代入方程得：-x2-2x+3=0，
解得：x1=-3，x2=1．
点评：本题考查了根的判别式，解一元二次方程的应用，题目是一道比较典型的题目，难度适中．
练习册系列答案
阅读快车系列答案
相关题目
甲、乙、丙三人共解出100道数学题，每人都解出其中的60道题；将其中只有1人解出的题叫做难题，3人都解出的叫做容易题，则（ ）
| A、难题比容易题少15道 |
| B、难题比容易题多15道 |
| C、难题比容易题少20道 |
| D、难题比容易题多20道 |
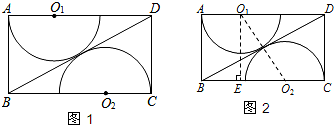问题：如图1，要在一个矩形木板ABCD上切割、拼接出一个圆形桌面，可在该木板上切割出半径相等的半圆形O1和半圆形O2，其中O1、O2分别是AD、BC上的点，半圆O1分别与AB、BD 相切，半圆O2分别与CD、BD相切．若AB=am，BC=bm，求最终拼接成的圆形桌面的半径（用含a、b的代数式表示）．