题目内容
17. 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.(1)画出直角坐标系;
(2)画出与△ABC关于x轴对称的图形△DEF;
(3)P为x轴上的一个动点,是否存在P使PA+PB的值最小?若不存在,请说明理由;若存在请求出点P的坐标和PA+PB的最小值.
分析 (1)根据C点坐标可确定原点位置,然后可画出坐标系;
(2)首先确定A、B、C三点关于x轴对称的对称点位置,然后连接即可;
(3)连接BD交x轴于点P,连接PA,设直线BD的表达式为y=kx+b,利用待定系数法确定解析式,然后根据解析式确定P点坐标,再利用勾股定理计算出BD的长.
解答 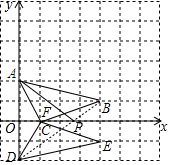 解:(1)如图所示:
解:(1)如图所示:
(2)如图所示:
(3)存在,连接BD交x轴于点P,连接PA,由对称可知D(0,-2),
设直线BD的表达式为y=kx+b,则有b=-2,4k+b=1,
解得:k=$\frac{3}{4}$,b=-2,
所以直线BD的表达式为y=$\frac{3}{4}$x-2,
当y=0时,有$\frac{3}{4}$x-2=0,
解得x=$\frac{8}{3}$,
所以P($\frac{8}{3}$,0),
由对称可知PA=PD,所以PA+PB=PD+PB=DB=$\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 此题主要考查了作图--轴对称变换,以及最短路线,关键是正确确定A、B、C三点关于x轴对称的对称点位置.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
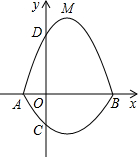 如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A,B为x轴上两点,C、D为y轴上的两点,经过点A,C,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.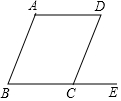 如图,已知AB∥CD,∠B=∠D,AD与BE平行吗?请说明理由.
如图,已知AB∥CD,∠B=∠D,AD与BE平行吗?请说明理由. 如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).
如图在Rt△ABC中,∠C=90°,翻折∠C使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).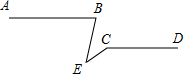 如图,AB∥CD,请探索∠B,∠C,∠E的关系?
如图,AB∥CD,请探索∠B,∠C,∠E的关系?