题目内容
14.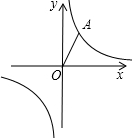 在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.(1)试确定此反比例函数的解析式;
(2)将线段OA绕O点顺时针旋转30°得到线段OB,判断点B是否在此反比例函数的图象上,并说明理由.
分析 (1)作AC⊥x轴于点C,在Rt△AOC中,解直角三角形求得A点坐标为(1,$\sqrt{3}$),把A(1,$\sqrt{3}$)分别代入代入y=$\frac{k}{x}$,根据待定系数法即可求得;
(2)作BD⊥x轴于点D,在Rt△BOD中,解直角三角形求得B点坐标为($\sqrt{3}$,1),把x=$\sqrt{3}$代入代入y=$\frac{\sqrt{3}}{x}$,即可判断.
解答 解:(1)作AC⊥x轴于点C,如图,
在Rt△AOC中,
∵OA=2,∠AOC=60°,
∴∠OAC=30°,
∴OC=$\frac{1}{2}$OA=1,AC=$\sqrt{3}$OC=$\sqrt{3}$,
∴A点坐标为(1,$\sqrt{3}$),
把A(1,$\sqrt{3}$)代入y=$\frac{k}{x}$,
得k=1×$\sqrt{3}$=$\sqrt{3}$,
∴反比例函数的解析式为y=$\frac{{\sqrt{3}}}{x}$;
(2)点B在此反比例函数的图象上,
理由如下:过点B作x轴的垂线交x轴于点D,
∵线段OA绕O点顺时针旋转30°得到线段OB,
∴∠AOB=30°,OB=OA=2,∴∠BOD=30°,
在Rt△BOD中,BD=$\frac{1}{2}$OB=1,OD=$\sqrt{3}$BD=$\sqrt{3}$,
∴B点坐标为($\sqrt{3}$,1),
∵当x=$\sqrt{3}$时,y=$\frac{{\sqrt{3}}}{x}$=1,
∴点B($\sqrt{3}$,1)在反比例函数y=$\frac{{\sqrt{3}}}{x}$的图象上.
点评 本题考查了反比例函数图象上点的坐标特征,解直角三角形,也考查了待定系数法求函数解析式.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.6月30日以来的强降雨造成某地洪灾.某市组织20辆汽车装运食品、药品和生活用品三种物质共100吨前往灾区.按计划20辆汽车都要装运,且每辆汽车只能装运同一种物质,且必须装满.根据下表提供的信息,解答下列问题.
(1)设装运食品的车辆数为x,装运药品的车辆数为y,求y与x的函数关系式;
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么有几种车辆安排方案?请写出所用的方案.
19.为了备战2016年里约奥运会,中国射击队正在积极训练.甲、乙两名运动员在相同的条件下,各射击10次.经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩方差是0.125,乙的成绩的方差是0.85,那么这10次射击中,甲、乙成绩的稳定情况是( )
| A. | 甲较为稳定 | B. | 乙较为稳定 | ||
| C. | 两个人成绩一样稳定 | D. | 不能确定 |
6.下面图形中是中心对称但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 长方形 | C. | 菱形 | D. | 正方形 |
3.在平面直角坐标系中.点P(1,-2)关于x轴对称的点的坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (-1,2) | D. | (-2,1) |
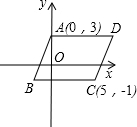 如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).
如图所示,在平面直角坐标系中,AD∥BC∥x轴,AD=BC=7,A(0,3),C(5,-1).