题目内容
4.解方程:(1)2x2-3x+1=0.
(2)x2-8x+1=0.(用配方法)
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)2x2-3x+1=0,
(2x-1)(x-1)=0,
2x-1=0,x-1=0,
x1=$\frac{1}{2}$,x2=1;
(2)x2-8x+1=0,
x2-8x=-1,
x2-8x+16=-1+16,
(x-4)2=15,
x-4=±$\sqrt{15}$,
x1=4+$\sqrt{15}$,x2=4-$\sqrt{15}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
相关题目
12. 某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:
某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:
八年级40名学生跳绳个数频数分布表
请结合图表完成下列问题:
(1)表中的m=13;
(2)请把频数分布直方图补充完整;
(3)已知八年级学生一分钟跳绳个数的成绩标准是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.如果该年级有360名学生,根据以上信息,请你估算该年级跳绳不合格的人数约为108名,成绩为优的人数约为27名.
 某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:
某学校为了解八年级学生的身体素质情况,随机抽取了八年级40名学生进行一分钟跳绳个数测试,以测试数据为样本,绘制出频数分布表和频数分布直方图,如图所示:八年级40名学生跳绳个数频数分布表
| 组别 | 分组/个 | 频数 |
| 第1组 | 80≤x<100 | 4 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | m |
| 第4组 | 140≤x<160 | 12 |
| 第5组 | 160≤x<180 | 3 |
(1)表中的m=13;
(2)请把频数分布直方图补充完整;
(3)已知八年级学生一分钟跳绳个数的成绩标准是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.如果该年级有360名学生,根据以上信息,请你估算该年级跳绳不合格的人数约为108名,成绩为优的人数约为27名.
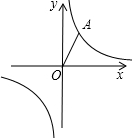 在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°.
在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$的图象经过点A,点O是坐标原点,OA=2且OA与x轴的夹角是60°. 有一块长20cm,宽10cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96cm2的无盖的盒子,求这个盒子的容积.
有一块长20cm,宽10cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为96cm2的无盖的盒子,求这个盒子的容积.
 如图,抛物线y=ax2+bx-4与x轴交于点A(-1,0)和点B(4,0),与y轴交于点C.
如图,抛物线y=ax2+bx-4与x轴交于点A(-1,0)和点B(4,0),与y轴交于点C.