Question

5．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，AB=8．
（1）利用尺规，作∠CAB的平分线，交⊙O于点D；（保留作图痕迹，不写作法）
（2）在（1）的条件下，连接CD，OD，若AC=CD，求∠B的度数；
（3）在（2）的条件下，OD交BC于点E，求由线段ED，BE，$\widehat{BD}$所围成区域的面积．（其中$\widehat{BD}$表示劣弧，结果保留π和根号）

Answer 1

分析 （1）由角平分线的基本作图即可得出结果；
（2）由等腰三角形的性质和圆周角定理得出∠CAD=∠B，再由角平分线得出∠CAD=∠DAB=∠B，由圆周角定理得出∠ACB=90°，得出∠CAB+∠B=90°，即可求出∠B的度数；
（3）证出∠OEB=90°，在Rt△OEB中，求出OE=$\frac{1}{2}$OB=2，由勾股定理求出BE，再由三角形的面积公式和扇形面积公式求出△OEB的面积=$\frac{1}{2}$OE•BE=2$\sqrt{3}$，扇形BOD的面积═$\frac{8π}{3}$，所求图形的面积=扇形面积-△OEB的面积，即可得出结果．

解答 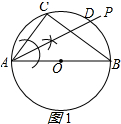解：（1）如图1所示，AP即为所求的∠CAB的平分线；
（2）如图2所示：
∵AC=CD，
∴∠CAD=∠ADC，
又∵∠ADC=∠B，
∴∠CAD=∠B，
∵AD平分∠CAB，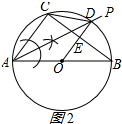
∴∠CAD=∠DAB=∠B，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CAB+∠B=90°，
∴3∠B=90°，
∴∠B=30°；
（3）由（2）得：∠CAD=∠BAD，∠DAB=30°，
又∵∠DOB=2∠DAB，
∴∠BOD=60°，
∴∠OEB=90°，
在Rt△OEB中，OB=$\frac{1}{2}$AB=4，
∴OE=$\frac{1}{2}$OB=2，
∴BE=$\sqrt{O{B}^{2}-O{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∴△OEB的面积=$\frac{1}{2}$OE•BE=$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$，扇形BOD的面积=$\frac{60π•{4}^{2}}{360}$=$\frac{8π}{3}$，
∴线段ED，BE，$\widehat{BD}$所围成区域的面积=$\frac{8π}{3}$-2$\sqrt{3}$．

点评 本题是圆的综合题目，考查了圆周角定理、等腰三角形的性质、勾股定理、扇形面积公式等知识；本题综合性强，有一定难度，熟练掌握圆周角定理是解决问题的关键．