题目内容
19.已知,D是正△ABC外接圆的弧BC上一点,求证:AD=BD+CD.分析 如图,在AD上截取DE=BD,连接BE,证得△BDE是等边三角形,得到BE=BD,∠BED=60°,由三角形的外角的性质得到∠AEB=∠BDC=120°,证得△ABE≌△BCD,根据全等三角形的性质得到AE=CD,等量代换即可得到结论.
解答  解:如图,在AD上截取DE=BD,连接BE,
解:如图,在AD上截取DE=BD,连接BE,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠ADB=∠ACB=60°,
∴△BDE是等边三角形,
∴BE=BD,∠BED=60°,
∴∠AEB=∠BDC=120°,
在△ABE与△BCD中,
$\left\{\begin{array}{l}{∠BAE=∠BCD}\\{∠AEB=∠BDC}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCD,
∴AE=CD,
∴AD=AE+DE=CD+BD.
点评 本题考查了圆周角定理,等边三角形的性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
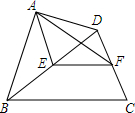 如图,在四边形ABCD中,AD⊥AB,BD=BC,点E、F分别是边BD、CD的中点,∠ABD=34°,∠DBC=40°,求∠EAF的度数.
如图,在四边形ABCD中,AD⊥AB,BD=BC,点E、F分别是边BD、CD的中点,∠ABD=34°,∠DBC=40°,求∠EAF的度数. 已知有理数a,b,c在数轴上对应的点的位置如图所示,化简|a-b|+3|c-a|-|b-c|.
已知有理数a,b,c在数轴上对应的点的位置如图所示,化简|a-b|+3|c-a|-|b-c|.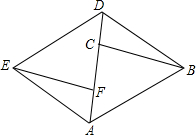 如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.
如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.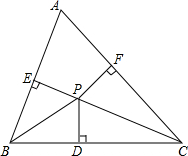 已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF.
已知△ABC内,∠ABC,∠ACB的角平分线交于点P,且PD,PE,PF分别垂直于BC,AC,AB于D,E,F三点.求证:PD=PE=PF. 如图,△ABC中,CA=CB,D在AC的延长线上,E在BC上,且CD=CE,求证:DE⊥AB.
如图,△ABC中,CA=CB,D在AC的延长线上,E在BC上,且CD=CE,求证:DE⊥AB. 将AD为12厘米的矩形纸片按图示折叠,使顶点C落在AB边上的点F,设∠CDE=α,求折痕DE的长.
将AD为12厘米的矩形纸片按图示折叠,使顶点C落在AB边上的点F,设∠CDE=α,求折痕DE的长.