题目内容
14.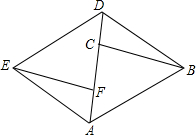 如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.
如图,AB∥ED,BC∥EF,点C、点F在AD上,AF=DC.(1)图中共有几对全等三角形?请分别写出来;
(2)选择其中一对全等的三角形加以证明.
分析 (1)根据平行线的性质可得∠DAB=∠FDE,∠BCF=∠EFD,然后可证明△ABC≌△DEF,进而可得ED=AB,然后可证明△EDA≌△BAD,进而可证明△DCB≌△AFE;
(2)根据平行线的性质可得∠DAB=∠FDE,∠BCF=∠EFD,再根据等式的性质可得DF=AC,然后可证明△ABC≌△DEF.
解答 解:(1)△ADB≌△DAE,△DEF≌△ABC,△EFA≌△BCD,共3对;
(2)∵AB∥ED,BC∥EF,
∴∠DAB=∠FDE,∠BCF=∠EFD,
∵AF=DC,
∴AF+CF=DC+CF,
∴DF=AC,
在△DEF和△ABC中$\left\{\begin{array}{l}{∠EDC=∠BAC}\\{AC=DF}\\{∠BCA=∠EFD}\end{array}\right.$,
∴△ABC≌△DEF(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.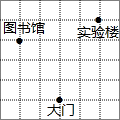 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
 如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )
如图所示,每个小方格的边长都为1,在直角坐标系中,如果图书馆的横坐标与实验楼的横坐标互为相反数,大门的纵坐标与实验搂的纵图坐标互为相反数,则图书馆的位置是( )| A. | (1,5) | B. | (-2,3) | C. | (-2,-1) | D. | (-2,1) |
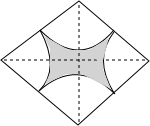 已知图中菱形的两条对角线长分别为8cm和6cm,影部分是由4条弧围成,这4条弧的圆心都是菱形的顶点,且半径都相等.该阴影部分的面积为(24-$\frac{25}{4}$π)cm2(结果保留π).
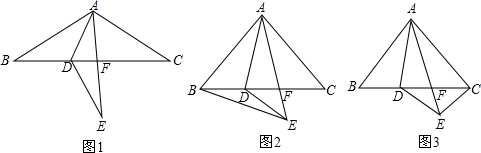
已知图中菱形的两条对角线长分别为8cm和6cm,影部分是由4条弧围成,这4条弧的圆心都是菱形的顶点,且半径都相等.该阴影部分的面积为(24-$\frac{25}{4}$π)cm2(结果保留π). 如图所示,已知△ABC中,AD是中线,猜想2AD与AB+AC大小关系,并说明理由.
如图所示,已知△ABC中,AD是中线,猜想2AD与AB+AC大小关系,并说明理由.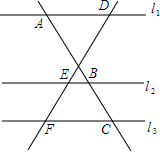 如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则DE•BC=6.
如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,则DE•BC=6.