题目内容
10.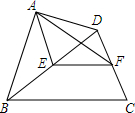 如图,在四边形ABCD中,AD⊥AB,BD=BC,点E、F分别是边BD、CD的中点,∠ABD=34°,∠DBC=40°,求∠EAF的度数.
如图,在四边形ABCD中,AD⊥AB,BD=BC,点E、F分别是边BD、CD的中点,∠ABD=34°,∠DBC=40°,求∠EAF的度数.
分析 根据直角三角形斜边上的中线等于斜边的一半可得AE=BE=$\frac{1}{2}$BD,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AED,再根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=$\frac{1}{2}$BC,然后根据两直线平行,同位角相等可得∠DEF=∠DBC,从而求出∠AEF,最后根据等腰三角形两底角相等求解即可.
解答 解:∵AD⊥AB,点E是BD的中点,
∴AE=BE=$\frac{1}{2}$BD,
∴∠BAE=∠ABD=34°,
∴∠AED=∠BAE+∠ABD=34°+34°=68°,
∵点E、F分别是边BD、CD的中点,
∴EF是△BCD的中位线,
∴EF∥BC且EF=$\frac{1}{2}$BC,
∴∠DEF=∠DBC=40°,
∴∠AEF=∠AED+∠DEF=68°+40°=108°,
又∵BD=BC,
∴AE=EF,
∴∠EAF=$\frac{1}{2}$(180°-∠AEF)=$\frac{1}{2}$(180°-108°)=36°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形两底角相等的性质,熟记各性质与定理并准确识图是解题的关键.

练习册系列答案
相关题目
15.如果a为有理数,那么下列各式一定为正数的是( )
| A. | |a| | B. | 2014a2 | C. | a2014 | D. | a2014+1 |
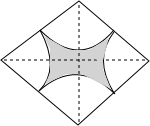 已知图中菱形的两条对角线长分别为8cm和6cm,影部分是由4条弧围成,这4条弧的圆心都是菱形的顶点,且半径都相等.该阴影部分的面积为(24-$\frac{25}{4}$π)cm2(结果保留π).
已知图中菱形的两条对角线长分别为8cm和6cm,影部分是由4条弧围成,这4条弧的圆心都是菱形的顶点,且半径都相等.该阴影部分的面积为(24-$\frac{25}{4}$π)cm2(结果保留π).