题目内容
19.已知a,b,c为△ABC的三边长,满足($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2=3($\sqrt{ab}$+$\sqrt{ac}$-$\sqrt{bc}$),试说明△ABC是等边三角形.分析 可将题目所给的可将题目所给的($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2=3($\sqrt{ab}$+$\sqrt{ac}$-$\sqrt{bc}$),进行适当变形,转换为几个完全平方式,然后根据非负数的性质求出a、b、c三边的数量关系,进而可判断出△ABC的形状.
解答 解:由($\sqrt{a}$+$\sqrt{b}$+$\sqrt{c}$)2=3($\sqrt{ab}$+$\sqrt{ac}$-$\sqrt{bc}$),
得:a+b+c-$\sqrt{ab}$-$\sqrt{ac}$-$\sqrt{bc}$=0,
则($\sqrt{a}$-$\sqrt{b}$)2+($\sqrt{b}$-$\sqrt{c}$)2+($\sqrt{c}$-$\sqrt{a}$)2=0,
所以a=b=c,
∴△ABC是等边三角形.
点评 本题考查了配方法的应用,关键是对要求的式子进行变形和因式分解,将已知的等式转化为偶次方的和,根据非负数的性质解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.m是方程x2+2x-2=0的根,则式子2m2+4m+2005的值为( )
| A. | 2009 | B. | 2007 | C. | 2008 | D. | 2010 |
7.如果|-n|=-n,下列成立的是( )
| A. | n>0 | B. | n<0 | C. | n>0或n=0 | D. | n<0或n=0 |
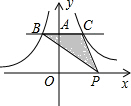 如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5.
如图,反比例函数$y=-\frac{3}{x}$和$y=\frac{7}{x}$上分别有两点B、C,且BC∥x轴,点P是x轴上一动点,则△BCP的面积是5.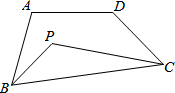 如图,在四边形ABCD中∠A+∠D=m°,∠ABC的平分线与∠BCD的平分线交于∠P,则∠P为$\frac{1}{2}$m°.
如图,在四边形ABCD中∠A+∠D=m°,∠ABC的平分线与∠BCD的平分线交于∠P,则∠P为$\frac{1}{2}$m°.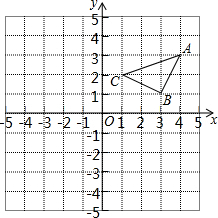 如图,将△ABC平移得到△A1B1C1,使A1点坐标为(1,1)
如图,将△ABC平移得到△A1B1C1,使A1点坐标为(1,1)