题目内容
11.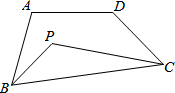 如图,在四边形ABCD中∠A+∠D=m°,∠ABC的平分线与∠BCD的平分线交于∠P,则∠P为$\frac{1}{2}$m°.
如图,在四边形ABCD中∠A+∠D=m°,∠ABC的平分线与∠BCD的平分线交于∠P,则∠P为$\frac{1}{2}$m°.
分析 先根据四边形内角和定理求出∠ABC+∠BCD的度数,然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数.
解答 解:∵四边形ABCD中,∠ABC+∠BCD=360°-(∠A+∠D)=360°-m°.
∵∠ABC的平分线与∠BCD的平分线交于∠P,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠BCD)=$\frac{1}{2}$(360°-m°)=180°-$\frac{1}{2}$m°,
则∠P=180°-(∠PBC+∠PCB)=180°-(180°-$\frac{1}{2}$m°)=$\frac{1}{2}$m°.
故答案为$\frac{1}{2}$m°.
点评 本题考查了多边形的内角和外角以及三角形、四边形的内角和定理,属于基础题.

练习册系列答案
相关题目
2.从A码头到B码头顺水航行原来需要行驶9小时,现在河道改变取直后,路程近了50千米,而船航行速度每小时增加40千米,结果只需6小时即可到达.若设A、B两码头之间改道后的航程为x千米,则可列方程为( )
| A. | 9(x-40)+50=6x | B. | 9(x-40)-50=6x | C. | $\frac{x+50}{9}$+40=$\frac{x}{6}$ | D. | $\frac{x+50}{9}$-40=$\frac{x}{6}$ |
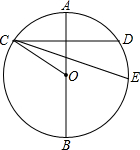 如图,AB为⊙O的一条固定直径,自左半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点E,当点C在左半圆(不包括A,B两点)上移动时,关于点E的说法:
如图,AB为⊙O的一条固定直径,自左半圆上一点C,作弦CD⊥AB,∠OCD的平分线交⊙O于点E,当点C在左半圆(不包括A,B两点)上移动时,关于点E的说法: 如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )
如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )