题目内容
有3张不透明的卡片,除正面分别写有不同的数字-1、-2、3外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数y=kx+b表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数y=kx+b表达式中的b.则一次函数y=kx+b的图象经过二、三、四象限的概率是 .
考点:列表法与树状图法,一次函数图象与系数的关系
专题:
分析:先根据题意列出树状图,再找出所有情况,看k<0,b<0的情况占总情况的多少即可求出答案.
解答:解:画树状图

共有6种情况,
因为一次函数y=kx+b经过第二、三、四象限,
则k<0,b<0,
又因为k<0,b<0的情况有k=-1,b=-2或k=-2,b=-1两种情况,
所以一次函数y=kx+b经过第二、三、四象限的概率为
=
;
故答案为:
.

共有6种情况,
因为一次函数y=kx+b经过第二、三、四象限,
则k<0,b<0,
又因为k<0,b<0的情况有k=-1,b=-2或k=-2,b=-1两种情况,
所以一次函数y=kx+b经过第二、三、四象限的概率为
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:此题考查了列表法与树状图,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
,注意本题是放回实验;经过二三四象限的一次函数的k<0,b<0.
| m |
| n |

练习册系列答案
相关题目
 如图,已知等边△ABC,P在AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证:
如图,已知等边△ABC,P在AC延长线上一点,以PA为边作等边△APE,EC延长线交BP于M,连接AM,求证: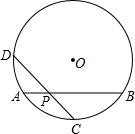 如图,在半径为6的⊙O中,弦AB的长为
如图,在半径为6的⊙O中,弦AB的长为
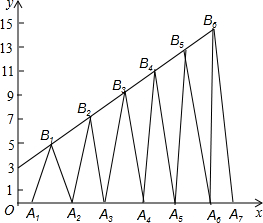 已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=
已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009= 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.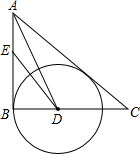 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3. 如图,过反比例函数
如图,过反比例函数