题目内容
已知n为正整数,二次方程x2+(2n+1)x+n2=0的两根为αn,βn,求下式的值:
+
+…+
.
| 1 |
| (α3+1)(β3+1) |
| 1 |
| (α4+1)(β4+1) |
| 1 |
| (α20+1)(β20+1) |
考点:根与系数的关系
专题:
分析:根据根与系数关系得αn+βn和αn•βn的值;把分母展开代值找规律计算.
解答:解:由韦达定理,有αn+βn=-(2n+1),αnβn=n2.
于是,对正整数n≥3,有
∴原式=
(1-
)+
(
-
)+…+
(
-
)
=
(1+
-
-
)
=
.
于是,对正整数n≥3,有
|
∴原式=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 18 |
| 1 |
| 20 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 19 |
| 1 |
| 20 |
=
| 531 |
| 760 |
点评:此题考查根与系数关系的综合应用,寻找规律是此题的关键,也是难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知四边形ABCD的对角线AC与BD相交于O,给出下列四个论断:①OA=OC;②AB=CD;③∠BAD=∠DCB;④AD∥BC.从中选择两个作为条件,以“四边形ABCD为平行四边形”作为结论,得到的6个命题中,真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
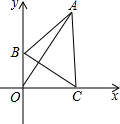 已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是
已知在平面直角系xOy中,三角形ABC是边长为a的等边三角形,并且边B点始终在y轴上,点C终在x轴上,则OA的最大值是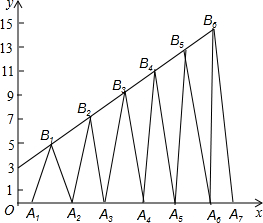 已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=
已知B1(1,y1)B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2011-S2009=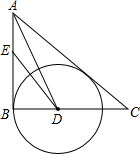 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.