题目内容
15.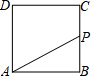 如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )| A. | 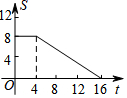 | B. | 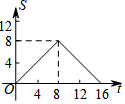 | C. | 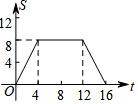 | D. | 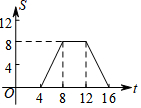 |
分析 分点P在AB、BC、CD、DA上运动这四种情况,根据三角形面积公式列出函数解析式,由函数解析式即可得出函数图象.
解答 解:当点P在AB上运动时,即0≤t≤4,S=$\frac{1}{2}$•t•0=0;
当点P在BC上运动时,即4<t≤8,S=$\frac{1}{2}$×4×(t-4)=2t-8;
当点P在CD上运动时,即8<t≤12,S=$\frac{1}{2}$×4×4=8;
当点P在DA上运动时,即12<t≤16,S=$\frac{1}{2}$×4×(16-t)=-2t+32;
符合以上四种情况的函数图象为D选项,
故选:D.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,利用数形结合的思想能得到各段三角形面积的变化规律.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
3.已知P1(-1,y1),P2(2,y2)是正比例函数y=-x图象上的两个点,则y1、y2的大小关系是( )
| A. | y1=y2 | B. | y1<y2 | C. | y1>y2 | D. | 不能确定 |
10.下列二元一次方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$的是( )
| A. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=0}\\{x-y=-4}\end{array}\right.$ |
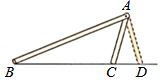 如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.
如图,△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等,这说明有两边和其中一边的对角分别相等的两个三角形不一定全等.
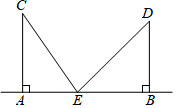 为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.
为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.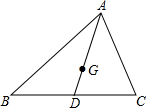 如图,AD为△ABC中线,点G为重心,若AD=9,则AG=6.
如图,AD为△ABC中线,点G为重心,若AD=9,则AG=6.