题目内容
5.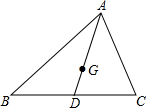 如图,AD为△ABC中线,点G为重心,若AD=9,则AG=6.
如图,AD为△ABC中线,点G为重心,若AD=9,则AG=6.
分析 首先根据重心到顶点的距离与重心到对边中点的距离之比为2:1,可得AG的长度是AD的长度的$\frac{2}{2+1}$;然后根据分数乘法的意义,用AD的长度乘以$\frac{2}{3}$,求出AG的长度是多少即可.
解答 解:∵重心到顶点的距离与重心到对边中点的距离之比为2:1,
∴AG=AD×$\frac{2}{2+1}$=9×$\frac{2}{3}$=6.
故答案为:6.
点评 此题主要考查了三角形的重心,要熟练掌握,解答此题的关键是要明确:重心到顶点的距离与重心到对边中点的距离之比为2:1.

练习册系列答案
相关题目
20. 如图,图中的同旁内角共有( )
如图,图中的同旁内角共有( )
 如图,图中的同旁内角共有( )
如图,图中的同旁内角共有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
11.下列变形中不正确的是( )
| A. | 若5x+8=4x,则5x-4x=8 | B. | 若3x-1=x+3,则2x=4 | ||
| C. | 若2=x,则x=2 | D. | 若x-1=3,则x=4 |
8.小明根据华师版八年级下册教材P37学习内容,对函数y=$\frac{1}{2}$x2的图象和性质进行了探究,试将如下尚不完整的过程补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
其中n=-3;
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
| x | … | -4 | n | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 4.5 | 2 | 0.5 | 0 | 0.5 | 2 | 4.5 | 8 | … |
(2)如图,在平面直角三角形坐标系xOy中,已描出了以上表中的部分数值为坐标的点,根据描出的点,画出该函数的大致图象.
(3)根据画出的函数图象,小明观察发现:该函数有最小值,没有最大值;当函数值取最小时,自变量x的值为0.
(4)进一步探究函数的图象发现:
①若点A(xa,ya),点B(xb,yb)在函数y=$\frac{1}{2}{x}^{2}$的图象上;
当xa<xb<0时,ya与yb的大小关系是ya>yb;
当0<xa<xb时,ya与yb的大小关系是ya<yb;
②直线y1恰好经过函数的图象上的点(-2,2)与(1,0.5);当y<y1时,x的取值范围是-2<x<1.

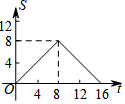
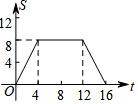
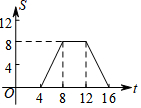
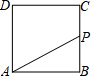 如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )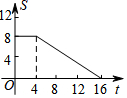
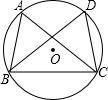 如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.
如图,点A,B,C,D是⊙O上的四点,且$\widehat{AB}$=$\widehat{CD}$,AC=DB.