题目内容
4.点A(-2,a),B(-1,b),C(3,c)在双曲线y=-$\frac{4}{x}$上,则a,b,c的大小关系为b>a>c.分析 根据点A、B、C的横坐标结合反比例函数图象上点的坐标特征即可求出a、b、c的值,比较后即可得出结论.
解答 解:∵点A(-2,a),B(-1,b),C(3,c)在双曲线y=-$\frac{4}{x}$上,
∴a=2,b=4,c=-$\frac{4}{3}$,
∵4>2>-$\frac{4}{3}$,
∴b>a>c.
故答案为:b>a>c.
点评 本题考查了反比例函数图象上点的坐标特征,利用反比例函数图象上点的坐标特征求出a、b、c的值是解题的关键.

练习册系列答案
相关题目
16.如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.把分式$\frac{x-2y+z}{xyz}$中的x、y、z都扩大到原来的2倍,那么分式的值( )
| A. | 不变 | B. | 扩大到原来的2倍 | C. | 缩小到原来的$\frac{1}{2}$ | D. | 缩小到原来的$\frac{1}{4}$ |
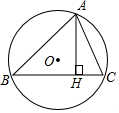 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24. 如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,则MN的值是5cm.
如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,则MN的值是5cm.