题目内容
15.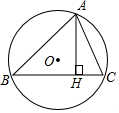 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24.
如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=20,AH=16,⊙O的半径为15,则AB=24.
分析 作直径AD,连接BD,根据圆周角定理得到∠ABD=90°,∠D=∠C,证明△ABD∽△AHC,根据相似三角形的性质解答即可.
解答 解: 作直径AD,连接BD,
作直径AD,连接BD,
∵AD为直径,
∴∠ABD=90°,又AH⊥BC,
∴∠ABD=∠AHC,
有圆周角定理得,∠D=∠C,
∴△ABD∽△AHC,
∴$\frac{AB}{AH}$=$\frac{AD}{AC}$,即$\frac{AB}{16}$=$\frac{30}{20}$,
解得,AB=24,
故答案为:24.
点评 本题考查的是三角形的外接圆和外心的概念和性质,掌握圆周角定理、相似三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.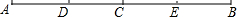 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
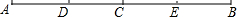 如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )
如图,C是AB的中点,D、E分别是AC、BC的中点,下列结论错误的是( )| A. | AC=2CE | B. | AB-AD=2CD | C. | AD=$\frac{1}{3}$DB | D. | DE=$\frac{1}{2}$AB |
6. 如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
 如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
3.-5的相反数是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
10.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得是白球的概率与不是白球的概率相同,那么m与n的关系是( )
| A. | m+n=4 | B. | m+n=8 | C. | m=n=4 | D. | m=3,n=5 |
20.单项式-$\frac{5x{y}^{2}}{3}$的系数与次数分别是( )
| A. | -5,2 | B. | -$\frac{1}{3}$,3 | C. | -$\frac{5}{3}$,2 | D. | -$\frac{5}{3}$,3 |