题目内容
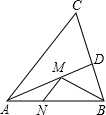 如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?
如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?考点:轴对称-最短路线问题
专题:
分析:作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值,由此可得出结论.
解答: 解:解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
解:解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∴当仅当BM垂直AC,MN垂直AB时BM+MN最小,该值为B到AC的距离.
 解:解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.
解:解:如图,作BH⊥AC,垂足为H,交AD于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AD是∠BAC的平分线,
∴M′H=M′N′,
∴BH是点B到直线AC的最短距离(垂线段最短),
∴当仅当BM垂直AC,MN垂直AB时BM+MN最小,该值为B到AC的距离.
点评:本题考查的是轴对称-最短路线问题,解答此类问题时要从已知条件结合图形认真思考,通过角平分线性质,垂线段最短,确定线段和的最小值.

练习册系列答案
相关题目
 如图,P为等边△ABC内任一点,设PA=x,PB=y,PC=z,AB=a.求证:x+y+z<2a.
如图,P为等边△ABC内任一点,设PA=x,PB=y,PC=z,AB=a.求证:x+y+z<2a. 如图,长方形的宽是a,则阴影部分的面积是
如图,长方形的宽是a,则阴影部分的面积是 如图,求四边形PABN的周长的最小值.
如图,求四边形PABN的周长的最小值.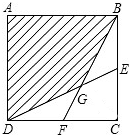 如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积.
如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是
如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是