题目内容
 如图,求四边形PABN的周长的最小值.
如图,求四边形PABN的周长的最小值.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:因为AB,PN的长度都是固定的,所以求出PA+NB的长度就行了.问题就是PA+NB什么时候最短.把B点向左平移2个单位到B′点;作B′关于x轴的对称点B″,连接AB″,交x轴于P,从而确定N点位置,此时PA+NB最短,再求出AB″+AB+PN的值即可.
解答: 解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),
解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),
则AB″=
=
,
∵A(1,-3),B(4,-1),P(a,0),N(a+2,0),
∴AB=
=
=
,PN=2,
∴四边形PABN的周长的最小值=
+
+2.
 解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),
解:将N点向左平移2单位与P重合,点B向左平移2单位到B′(2,-1),作B′关于x轴的对称点B″,根据作法知点B″(2,1),则AB″=
| (1-2)2+(-3-1)2 |
| 17 |
∵A(1,-3),B(4,-1),P(a,0),N(a+2,0),
∴AB=
| (1-4)2+(-3+1)2 |
| 9+4 |
| 13 |
∴四边形PABN的周长的最小值=
| 17 |
| 13 |
点评:本题考查的是轴对称-最短路线问题,熟知“两点之间,线段最短”是解答此题的关键.

练习册系列答案
相关题目

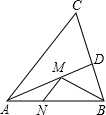 如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?
如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值? 在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,AB=13,CD=6,则tanA=
在Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,AB=13,CD=6,则tanA=