题目内容
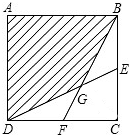 如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积.
如图,已知正方形ABCD的边长为3,E、F分别是BC、DC的中点,BF、DE相交于点G,求四边形ABGD的面积.考点:正方形的性质
专题:
分析:连接BD,可看出阴影部分的面积等于
正方形的面积+一个三角形的面积,用相似求出三角形的面积,阴影部分的面积可证.
| 1 |
| 2 |
解答: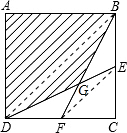 解:连接BD,EF.
解:连接BD,EF.
∵阴影部分的面积=△ABD的面积+△BDG的面积,
∴△ABD的面积=
正方形ABCD的面积=
×32=
,
∵△BCD中EF为中位线,
∴EF∥BD,EF=
BD,
∴△GEF∽△GBD,
∴DG=2GE,
∴△BDE的面积=
△BCD的面积.
∴△BDG的面积=
△BDE的面积=
△BCD的面积=
×
×32=
.
∴阴影部分的面积=
+
=6.
 解:连接BD,EF.
解:连接BD,EF.∵阴影部分的面积=△ABD的面积+△BDG的面积,
∴△ABD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∵△BCD中EF为中位线,
∴EF∥BD,EF=
| 1 |
| 2 |
∴△GEF∽△GBD,
∴DG=2GE,
∴△BDE的面积=
| 1 |
| 2 |
∴△BDG的面积=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 9 |
| 6 |
∴阴影部分的面积=
| 9 |
| 2 |
| 9 |
| 6 |
点评:本题考查正方形的性质,正方形的四个边长相等,关键是连接BD,把阴影部分分成两部分计算.

练习册系列答案
相关题目
如果(x+a)(x+b)的积中不含x的一次项,那么a、b一定是( )
| A、ab=1 |
| B、a+b=0 |
| C、a=0或b=0 |
| D、ab=0 |
 如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是
如图,ABCD是一个正方形,△APM的面积是15,CNR的面积是12,四边形PQRD的面积是51,则四边形BMQN的面积是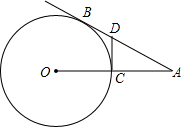 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=2,求⊙O的半径.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,过点C的切线交AB于点D.若AD=2BD,CD=2,求⊙O的半径.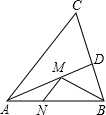 如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?
如图,在锐角△ABC,∠BAC的角平分线交BC于点D,M、N分别是AD、AB上的动点,当M、N在何位置时,BM+MN取得最小值?