题目内容
2.先化简,再求值:($\frac{x}{x+2}$-$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$)÷$\frac{x}{x+2}$,其中x=$\sqrt{2}$.分析 原式括号中利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{{x}^{2}-2x-{x}^{2}+4x-4}{(x+2)(x-2)}$•$\frac{x+2}{x}$=$\frac{2(x-2)}{(x+2)(x-2)}$•$\frac{x+2}{x}$=$\frac{2}{x}$,
当x=$\sqrt{2}$时,原式=$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在直角坐标系中,点(-2,3)关于x轴的对称点的坐标是( )
| A. | (-2,-3) | B. | (-2,3) | C. | (2,-3) | D. | (2,3) |
13.若关于x的一元二次方程2x2-ax+1=0的一个解是x=-1,则a的值是( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
7.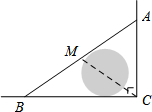 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
 如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )
如图,公路AC、BC互相垂直,公路AB的中点M与点C被湖隔开.若测得BM的长为1.2km,则点M与点C之间的距离为( )| A. | 0.5km | B. | 0.6km | C. | 0.9km | D. | 1.2km |
 如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.
如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.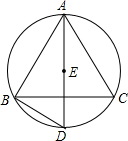 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.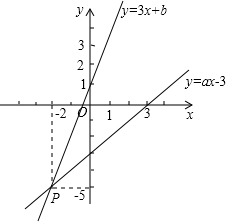 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得方程组$\left\{\begin{array}{l}{3x-y=-b}\\{ax-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得方程组$\left\{\begin{array}{l}{3x-y=-b}\\{ax-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.