题目内容
14.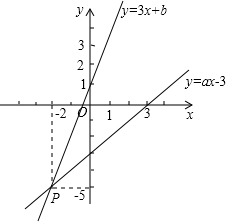 如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得方程组$\left\{\begin{array}{l}{3x-y=-b}\\{ax-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.
如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得方程组$\left\{\begin{array}{l}{3x-y=-b}\\{ax-y=3}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.
分析 利用函数图象交点坐标为两函数解析式组成的方程组的解即可得到答案.;
解答 解:因为函数y=3x+b和y=ax-3的图象交于点P(-2,-5),
所以方程组$\left\{\begin{array}{l}{3x-y=-b}\\{ax-y=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x=-2}\\{y=-5}\end{array}\right.$.
点评 本题主要考查一次函数函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
5.下面计算正确的是( )
| A. | 6a-5a=1 | B. | a+2a2=3a2 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
19.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | 3a2+a2=4a4 | C. | a2b-ba2=0 | D. | 4a2-5a2=-1 |
4.如果代数式3-x|m|-1+(m+1)x是关于x的二次三项式,那么m的值为( )
| A. | ±3 | B. | 1 | C. | -1 | D. | 2 |
 如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b.
如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b.