题目内容
17.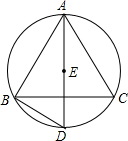 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.(1)当△ABC的外接圆半径为1时,且∠BAC=60°,求弧BC的长度.
(2)连接BD,求证:DE=DB.
分析 (1)设△ABC的外接圆的圆心为O,连接OB、OC,由圆周角定理得出∠BOC=120°,再由弧长公式即可得出结果;
(2)连接BE,由三角形的内心得出∠1=∠2,∠3=∠4,再由三角形的外角性质和圆周角定理得出∠DEB=∠DBE,即可得出结论.
解答 (1)解:设△ABC的外接圆的圆心为O,连接OB、OC,如图1所示: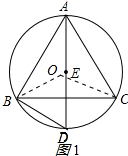
∵∠BAC=60°,
∴∠BOC=120°,
∴弧BC的长度=$\frac{120π×1}{180}$=$\frac{2}{3}π$.
(2)证明:连接BE,如图2所示:
∵E是△ABC的内心,
∴∠1=∠2,∠3=∠4,
∵∠DEB=∠1+∠3,∠DBE=∠4+∠5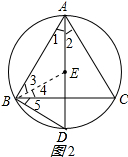
∠5=∠2,
∴∠DEB=∠DBE,
∴DE=DB.
点评 本题考查了三角形的外心与内心、圆周角定理、弧长公式、三角形的外角性质、等腰三角形的判定等知识;本题综合性强,根据圆周角定理得出角的数量关系是解题的关键.

练习册系列答案
相关题目
7.已知α,β是一元二次方程x2-5x-2=0的两个不相等的实数根,则α+β+αβ的值为( )
| A. | -1 | B. | 9 | C. | 3 | D. | 27 |
5.下面计算正确的是( )
| A. | 6a-5a=1 | B. | a+2a2=3a2 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
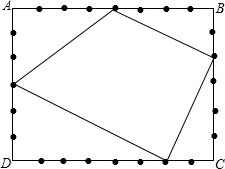 如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法.
如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法. 如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b.
如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b. 一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考:
一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考: