题目内容
已知△ABC中,D、E分别是AB、AC上的点,AD=2,AB=6,AC=4,要使△ABC和△ADE相似,则AE的长为 .
考点:相似三角形的判定
专题:
分析:分①AD与AB是对应边,②AD与AC是对应边两种情况,利用相似三角形对应边成比例列出比例式求解即可.
解答: 解:①AD与AB是对应边时,如图1,
解:①AD与AB是对应边时,如图1,
∵△ADE∽△ABC,
∴
=
,
即
=
,
解得AE=
;
②AD与AC是对应边时,如图2,
∵△ADE∽△ABC,
∴
=
,
即
=
,
解得AE=3,
综上,AE=
或3.
故答案为:
或3.
 解:①AD与AB是对应边时,如图1,
解:①AD与AB是对应边时,如图1,∵△ADE∽△ABC,
∴
| AD |
| AB |
| AE |
| AC |
即
| 2 |
| 6 |
| AE |
| 4 |
解得AE=
| 4 |
| 3 |
②AD与AC是对应边时,如图2,
∵△ADE∽△ABC,
∴
| AD |
| AC |
| AE |
| AB |
即
| 2 |
| 4 |
| AE |
| 6 |
解得AE=3,
综上,AE=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查了相似三角形对应边成比例的性质,难点在于要根据对应边分情况讨论求解.

练习册系列答案
相关题目
正方形具有而菱形不具有的性质是( )
| A、内角和为360° |
| B、对角线互相垂直平分 |
| C、对角线相等 |
| D、对角线平分内角 |
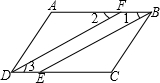 请把下面证明过程补充完整:
请把下面证明过程补充完整:
 如图,在等腰梯形ABCD中,AD∥BC,AB=AD=DC,∠B=60°,NC=
如图,在等腰梯形ABCD中,AD∥BC,AB=AD=DC,∠B=60°,NC=