题目内容
13.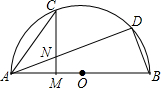 如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.
如图所示,D是以AB为直径的半圆O上的一点,C是弧AD的中点,点M在AB上,AD与CM交于点N,CN=AN.(1)求证:CM⊥AB;
(2)若AC=$2\sqrt{3}$;,BD=2,求半圆的直径.
分析 (1)连接BC,根据圆周角定理和三角形相似即可得到结论.
(2)连接CD,作CE⊥BD,交BD的延长线于E,通过△CMB≌△CEB,得到ED=AM,根据射影定理即可求出结论.
解答  (1)证明:如图1,连接BC,则∠ACB=90°,
(1)证明:如图1,连接BC,则∠ACB=90°,
∵CN=AN,
∴∠NCA=∠NAC,
∴∠MCA=∠DAC,
∵C是弧AD的中点,
∴∠ABC=∠DAC,
∴∠MCA=∠ABC,
∵∠CAB=∠BAC,
∴△ABC∽△ACM,
∴∠AMC=90°,
∴CM⊥AB;
(2)解:如图2,连接CD,作CE⊥BD,交BD的延长线于E,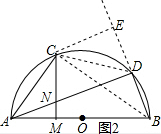
在△CMB与△BCE中,
$\left\{\begin{array}{l}{∠MBC=∠CBE}\\{∠CMB=∠CEB}\\{BC=BC}\end{array}\right.$,
∴△CMB≌△CEB,
∴BM=BE,CM=CE,
∵C是弧AD的中点,
∴AC=CD,
在Rt△ACM与Rt△CED中,$\left\{\begin{array}{l}{AC=CD}\\{CM=CE}\end{array}\right.$,
∴Rt△ACM≌Rt△CED,
∴AM=DE,
设AM=x,则BM=BE=BD+DE=2+x,
∴AB=AM+BM=2+2x,
∵∠ACB=∠AMC=90°,
∴AC2=AM•AB,
∴12=x(2+2x),
解得:x=2,
∴AB=6.
点评 本题考查了相似三角形的判定和性质,圆周角定理,全等三角形的判定与性质,射影定理,作辅助线构造全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列整式能直接利用完全平方公式分解因式的是( )
| A. | x2-4 | B. | x2+6x+9 | C. | x2-2x-1 | D. | x2+y2 |
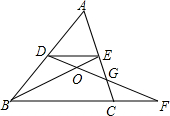 如图所示,在三角形ABC中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DE交于点O.若△ADE的面积为2,则四边形BOGC的面积为$\frac{7}{2}$.
如图所示,在三角形ABC中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DE交于点O.若△ADE的面积为2,则四边形BOGC的面积为$\frac{7}{2}$. 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点.