题目内容
5．利用函数图象解方程组$\left\{\begin{array}{l}{y=x+3}\\{y=2x+1}\end{array}\right.$．分析 在同一平面直角坐标系中画出函数y=x+3与y=2x+1的图象，两直线交点的坐标就是方程组$\left\{\begin{array}{l}{y=x+3}\\{y=2x+1}\end{array}\right.$的解．
解答 解：如图：两个函数的交点坐标是（2，5），则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$．
点评 本题考查的是一次函数与二元一次方程（组），解答此题的关键是正确画出两个一次函数的图象，找出两直线的交点坐标．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
如图所示，一根旗杆被风刮倒，从离地面8米的A处断裂，旗杆顶落在地面距离底部C点15米的B处，则旗杆在断裂之前有多高？
16．$\sqrt{（-4）^{2}}$的平方根与$\root{3}{-8}$的和的绝对值是（ ）
| A． | 0 | B． | 4 | C． | 0或2 | D． | 4或0 |
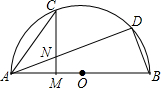如图所示，D是以AB为直径的半圆O上的一点，C是弧AD的中点，点M在AB上，AD与CM交于点N，CN=AN．
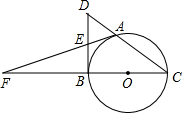如图 A是以BC为直径的⊙O上一点，过点B作⊙O的切线，与CA的延长线交于点D，E是BD的中点，延长AE与CB的延长线相交于点F．求证：AF是⊙O的切线．
如图，在△ABC和△DCE中，AB∥DC，AB=DC，BC=CE，且点B，C，E在一条直线上．求证：∠A=∠D．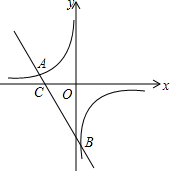
如图所示，直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B，与x轴交于点C．