题目内容
12.菱形的周长为16cm,两相邻内角的度数之比为1:2,则该菱形的面积是8$\sqrt{3}$cm2.分析 如图,四边形ABCD为菱形,∠B:∠BAC=1:2,根据菱形的性质得AB=BC=,BC∥AD,接着利用平行线的性质得∠B+∠BAC=180°,于是可计算出∠B=60°,则可判断△ABC为等边三角形,然后根据菱形得性质和等边三角形的面积公式求解.
解答 解: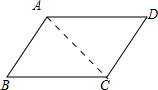 如图,四边形ABCD为菱形,∠B:∠BAC=1:2,
如图,四边形ABCD为菱形,∠B:∠BAC=1:2,
∵四边形ABCD为菱形,
∴AB=BC=,BC∥AD,
∴∠B+∠BAC=180°,
即∠B+2∠B=180°,
∴∠B=60°,
∴△ABC为等边三角形,
∴菱形ABCD的面积=2S△ABC=2×$\frac{\sqrt{3}}{4}$×42=8$\sqrt{3}$(cm2).
故答案为8$\sqrt{3}$cm2.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积为对角线乘积的一半.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.扇形的圆心角是100°,弧长为20πcm,则扇形的面积为( )
| A. | 180πcm2 | B. | 240πcm2 | C. | 320πcm2 | D. | 360πcm2 |
2.下列运算正确的是( )
| A. | x2•x3=x6 | B. | $\root{3}{-8}$=2 | C. | (-2)0=0 | D. | 2-1=$\frac{1}{2}$ |