题目内容
3.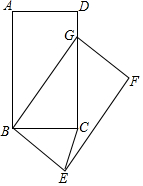 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.
分析 连接AG,根据旋转变换的性质得到,∠ABG=∠CBE,BA=BG,根据勾股定理求出CG、AD,根据相似三角形的性质列出比例式,计算即可.
解答 解: 连接AG,
连接AG,
由旋转变换的性质可知,∠ABG=∠CBE,BA=BG=5,BC=BE,
由勾股定理得,CG=$\sqrt{B{G}^{2}-B{C}^{2}}$=4,
∴DG=DC-CG=1,
则AG=$\sqrt{A{D}^{2}+D{G}^{2}}$=$\sqrt{10}$,
∵$\frac{BA}{BC}$=$\frac{BG}{BE}$,∠ABG=∠CBE,
∴△ABG∽△CBE,
∴$\frac{CE}{AG}$=$\frac{BC}{AB}$=$\frac{3}{5}$,
解得,CE=$\frac{3\sqrt{10}}{5}$,
故答案为:$\frac{3\sqrt{10}}{5}$.
点评 本题考查的是翻转变换的性质、相似三角形的判定和性质,掌握勾股定理、矩形的性质、旋转变换的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.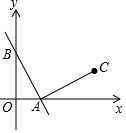 如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )
如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )
 如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )
如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )| A. | (2,1) | B. | (1,2) | C. | (3,1) | D. | (1,3) |
8. 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )| A. | 0.6x+0.4y+100=500 | B. | 0.6x+0.4y-100=500 | ||
| C. | 0.4x+0.6y+100=500 | D. | 0.4x+0.6y-100=500 |
15.若关于x的一元二次方程x2+mx+m-4=0有一根为0,则m的值为( )
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
12.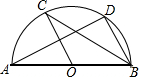 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
 如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )
如图,AB是⊙O的直径,C、D是⊙O上的点,且OC∥BD,∠A=30°,则∠CBD=( )| A. | 10° | B. | 15° | C. | 30° | D. | 45° |