题目内容
14.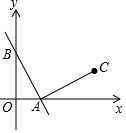 如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )
如图,函数y=-2x+2的图象分别与x轴、y轴交于A,B两点,线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为( )| A. | (2,1) | B. | (1,2) | C. | (3,1) | D. | (1,3) |
分析 过C点作CD⊥x轴于D,如图,先利用一次函数图象上点的坐标特征确定B(0,2),A(1,0),再证明△ABO≌△CAD,得到AD=OB=2,CD=OA=1,则C点坐标可求.
解答 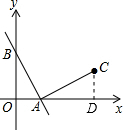 解:过C点作CD⊥x轴于D,如图.
解:过C点作CD⊥x轴于D,如图.
∵y=-2x+2的图象分别与x轴、y轴交于A,B两点,
∴当x=0时,y=2,则B(0,2),
当y=0时,-2x+2=0,解得x=1,则A(1,0).
∵线段AB绕A点顺时针旋转90°,
∴AB=AC,∠BAC=90°,
∴∠BAO+∠CAD=90°,
而∠BAO+∠ABO=90°,
∴∠ABO=∠CAD.
在△ABO和△CAD中
$\left\{\begin{array}{l}{∠AOB=∠CDA}\\{∠ABO=∠CAD}\\{AB=CA}\end{array}\right.$,
∴△ABO≌△CAD,
∴AD=OB=2,CD=OA=1,
∴OD=OA+AD=1+2=3,
∴C点坐标为(3,1).
故选C.
点评 本题考查的是一次函数图象与几何变换,旋转的性质,一次函数图象上点的坐标特征,全等三角形的判定与性质,证明△ABO≌△CAD是解答此题的关键.

练习册系列答案
相关题目
4.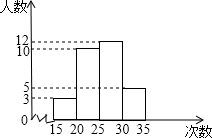 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )| A. | 0.2 | B. | 0.17 | C. | 0.33 | D. | 0.14 |
2.济宁市人口约为530060人,用科学记数法可表示为( )
| A. | 53006×10人 | B. | 0.53×106人 | C. | 5.3006×105人 | D. | 53×104人 |
6.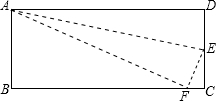 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
 如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.
如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2.| A. | 16.9 | B. | 14.4 | C. | 13.5 | D. | 11.8 |
4.若(2x+3y-12)2+|x-2y+1|=0,则xy=( )
| A. | 9 | B. | 12 | C. | 27 | D. | 64 |
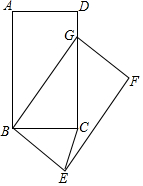 如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.
如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是$\frac{3\sqrt{10}}{5}$.