题目内容
周末,小军(用A表示)、小明(用B表示)、小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁有四个座位,A先坐下来,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而坐的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:列表法与树状图法
专题:
分析:首先可设第一个位置和第三个位置都与A相邻.然后根据题意画树状图,再由树状图求得所有等可能的结果与A与B不相邻而坐的情况,然后利用概率公式求解即可求得答案.
解答:解:可设第一个位置和第三个位置都与A相邻.

∵共有6种等可能的结果,A与B不相邻而坐的有2种情况,
∴A与B不相邻而坐的概率为:
=
.
故选B.

∵共有6种等可能的结果,A与B不相邻而坐的有2种情况,
∴A与B不相邻而坐的概率为:
| 2 |
| 6 |
| 1 |
| 3 |
故选B.
点评:此题考查了树状图法与列表法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
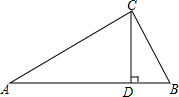 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
式子
在实数范围内有意义,则x的取值范围是( )
| x+2 |
| A、x>-2 | B、x≥-2 |
| C、x<-2 | D、x≤-2 |
下列运算正确的是( )
| A、4a2b-3a2b=1 |
| B、4a2b×3a2b=12a4b2 |
| C、(2a2)3=6a6 |
| D、(a+b)2=a2+b2 |

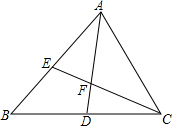 如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证:
如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证: