题目内容
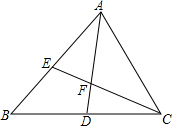 如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证:
如图,在△ABC中,点D是BC中点,点E是AB上任意一点(除A,B外),AD与CE相交于点F,求证:| AE |
| EB |
| AF |
| 2FD |
考点:相似三角形的判定与性质
专题:证明题
分析:过点D作DG∥CE,判断出DG是△BCE的中位线,从而得到GE=
EB,再求出△AEF和△AGD相似,利用相似三角形对应边成比例列式整理即可得证.
| 1 |
| 2 |
解答: 证明:如图,过点D作DG∥CE,
证明:如图,过点D作DG∥CE,
∵点D是BC的中点,
∴DG是△BCE的中位线,
∴GE=
EB,
∵DG∥CE,
∴△AEF∽△AGD,
∴
=
,
即
=
,
∴
=
.
 证明:如图,过点D作DG∥CE,
证明:如图,过点D作DG∥CE,∵点D是BC的中点,
∴DG是△BCE的中位线,
∴GE=
| 1 |
| 2 |
∵DG∥CE,
∴△AEF∽△AGD,
∴
| AE |
| GE |
| AF |
| FD |
即
| AE | ||
|
| AF |
| FD |
∴
| AE |
| EB |
| AF |
| 2FD |
点评:本题考查了相似三角形的判定与性质,三角形的中位线定理,熟练掌握三角形相似的判定方法并作辅助线构造出相似三角形是解题的关键.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
周末,小军(用A表示)、小明(用B表示)、小华(用C表示)和小张(用D表示)一起到图书馆看书,圆桌旁有四个座位,A先坐下来,B、C、D三人随机坐到其他三个座位上,则A与B不相邻而坐的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°∠CAE=65°,∠E=70°,且AD⊥BC,则∠BAC的度数为( )| A、60° | B、75° |
| C、90° | D、85° |
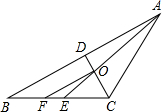 如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )
如图,在△ABC中,∠BAC、∠ACB的平分线交于点O.若AC=BC,OF∥AB,则下列结论中不正确的是( )A、∠OAB=
| ||
| B、∠OEC=∠OCE | ||
C、∠OAB=
| ||
| D、OC⊥OF | ||
| E、∠OEC=∠OCE |
 如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.
如图,已知直线AB=10,点O在AB上,射线OC垂直平分线段AB,点P在射线OC上运动,设OP=x.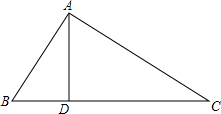 如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,BD=3,CD=8,求AB的长.
如图,在△ABC中,AD⊥BC于D,且∠CAD=2∠BAD,BD=3,CD=8,求AB的长. 如图,在△ABC中,∠B=∠C,AD为BC上的中线,DE⊥AB于点E,DF⊥AC于点F,求证:DA平分∠EDF.
如图,在△ABC中,∠B=∠C,AD为BC上的中线,DE⊥AB于点E,DF⊥AC于点F,求证:DA平分∠EDF. 如图,△ABC是等边三角形,过它的三个顶点分别作为对边的平行线,得到一个新的△DEF,△DEF是等边三角形?你还能找到其他的等边三角形?点A、B、C分别是EF、ED、FD的中点吗?请证明你的结论.
如图,△ABC是等边三角形,过它的三个顶点分别作为对边的平行线,得到一个新的△DEF,△DEF是等边三角形?你还能找到其他的等边三角形?点A、B、C分别是EF、ED、FD的中点吗?请证明你的结论.