题目内容
12. 如图,OA⊥OC,∠AOB=∠COD,求∠BOD的度数.
如图,OA⊥OC,∠AOB=∠COD,求∠BOD的度数.
分析 根据OA⊥OC,可得∠AOB与∠BOC互余,再根据∠AOB=∠COD,可得∠COD与∠BOC互余,据此可得∠BOD的度数.
解答 解:∵OA⊥OC,
∴∠AOB与∠BOC互余,
又∵∠AOB=∠COD,
∴∠COD与∠BOC互余,
∴∠BOD=90°.
点评 本题主要考查了垂线的定义以及余角的定义的运用,解题时注意:如果两个角的和等于90°(直角),就说这两个角互为余角,其中一个角是另一个角的余角.

练习册系列答案
相关题目
7.在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
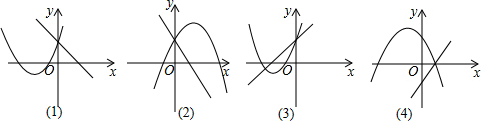

| A. | (4) | B. | (1),(4) | C. | (2),(3) | D. | (3),(4) |
2.若∠α=36°17′28″,∠β=42°57′40″,则∠α+∠β=( )
| A. | 78°15′8″ | B. | 78°14′8″ | C. | 79°15′8″ | D. | 79°14′8″ |
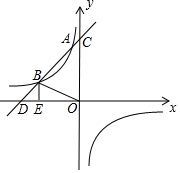 如图,直线y=mx+4交x轴于D,交y轴于C,交双曲线y=$\frac{k}{x}$在第二象限交于点A和点B(-3,n),且S△OBE=$\frac{3}{2}$.
如图,直线y=mx+4交x轴于D,交y轴于C,交双曲线y=$\frac{k}{x}$在第二象限交于点A和点B(-3,n),且S△OBE=$\frac{3}{2}$. 某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元,小王携带现金3000元到这市场购苹果,并以批发价买进,如果购买的苹果为x千克,小王付款后的剩余现金为y元.
某水果批发市场规定,批发苹果不少于100千克时,批发价为每千克2.5元,小王携带现金3000元到这市场购苹果,并以批发价买进,如果购买的苹果为x千克,小王付款后的剩余现金为y元.