题目内容
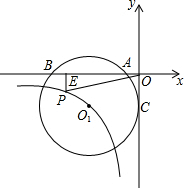 如图,⊙O1与y轴切于点C(0,-2),与x轴负半轴交于A、B两点,A(-1,0),双曲线y=
如图,⊙O1与y轴切于点C(0,-2),与x轴负半轴交于A、B两点,A(-1,0),双曲线y=| k |
| x |
考点:圆的综合题
专题:综合题
分析:作O1H⊥AB于H,如图,设⊙O1的半径为r,由于⊙O1与y轴切于点C,根据切线性质得O1C⊥y轴,O1C=r,易判断四边形O1COH为矩形,所以O1H=OC=2,OH=O1C=r,在Rt△AO1H中,利用勾股定理得到22+(r-1)2=r2,解得r=
,则得到点O1的坐标为(-
,-2),根据反比例函数图象上点的坐标特征得k=5,即反比例函数解析式为y=
,然后根据反比例函数k的几何意义即可得到S△PEO.
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| x |
解答:解:作O1H⊥AB于H,如图,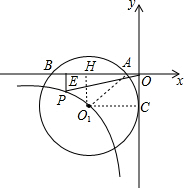 设⊙O1的半径为r,
设⊙O1的半径为r,
∵⊙O1与y轴切于点C,
∴O1C⊥y轴,O1C=r,
∴四边形O1COH为矩形,
∴O1H=OC=2,OH=O1C=r,
在Rt△AO1H中,O1A=r,AH=OH-OA=r-1,
∵O1H2+AH2=O1A2,
∴22+(r-1)2=r2,解得r=
,
∴点O1的坐标为(-
,-2),
∵双曲线y=
过点O1,
∴k=-
×(-2)=5,
即反比例函数解析式为y=
,
∴S△PEO=
|k|=
.
 设⊙O1的半径为r,
设⊙O1的半径为r,∵⊙O1与y轴切于点C,
∴O1C⊥y轴,O1C=r,
∴四边形O1COH为矩形,
∴O1H=OC=2,OH=O1C=r,
在Rt△AO1H中,O1A=r,AH=OH-OA=r-1,
∵O1H2+AH2=O1A2,
∴22+(r-1)2=r2,解得r=
| 5 |
| 2 |
∴点O1的坐标为(-
| 5 |
| 2 |
∵双曲线y=
| k |
| x |
∴k=-
| 5 |
| 2 |
即反比例函数解析式为y=
| 5 |
| x |
∴S△PEO=
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了圆的综合题:熟练掌握圆的切线性质和反比例函数k的几何意义;会利用勾股定理建立等量关系求未知量;理解坐标与图形性质.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
把一个正方形纸片折叠三次后沿虚线剪断①②两部分,则展开①后得到的是( )


A、 |
B、 |
C、 |
D、 |
在数轴上与表示-3的点的距离等于5的点所表示的数是( )
| A、-8和2 | B、8和-2 |
| C、-8和-2 | D、8和2 |
 如图,要焊接一个高为3.5m,底角为32°的人字形钢架(等腰三角形),约需多长的钢材?(精确到0.01m)
如图,要焊接一个高为3.5m,底角为32°的人字形钢架(等腰三角形),约需多长的钢材?(精确到0.01m)
 如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E.
如图,在△ABC中,AB=AC,D为BC边上一点,连接AD并延长,与三角形ABC的外接圆交于点E.